By Natasha Diederen, Alice Mehalek, Zhecheng Wang, and Olga Guțan
This week we worked on extending the results described here. We learned an array of new techniques and enhanced existing skills that we had developed the week(s) before. Here is some of the work we have accomplished since the last blog post.
Tiling
One of the improvements we made was to create a tiling function which created an \( n^3 \) grid of our triply periodic surfaces, so that we were better able to visualise them as a structure. We started off with a surface inside a \( [-1, 1]^3 \) cube, and then imagined an \(n^3\) grid (pictured below). To make a duplicate of the surface in one of these grid cubes, we considered how much the surface would need to be translated in the \(x\), \(y\) and \(z\) directions. For example to duplicate the original surface in the black cube into the green square, we would need to shift all the \(x\)-coordinates in the mesh by two (since the cube is length two in all directions) and leave the \(y\)- and \(z\)-coordinates unchanged. Similarly, to duplicate the original surface into the purple square, we would need to shift the all \(x\)-coordinates in the mesh by two, all the \(y\)-coordinates by two, and all the \(z\)-coordinates by \(2n\).
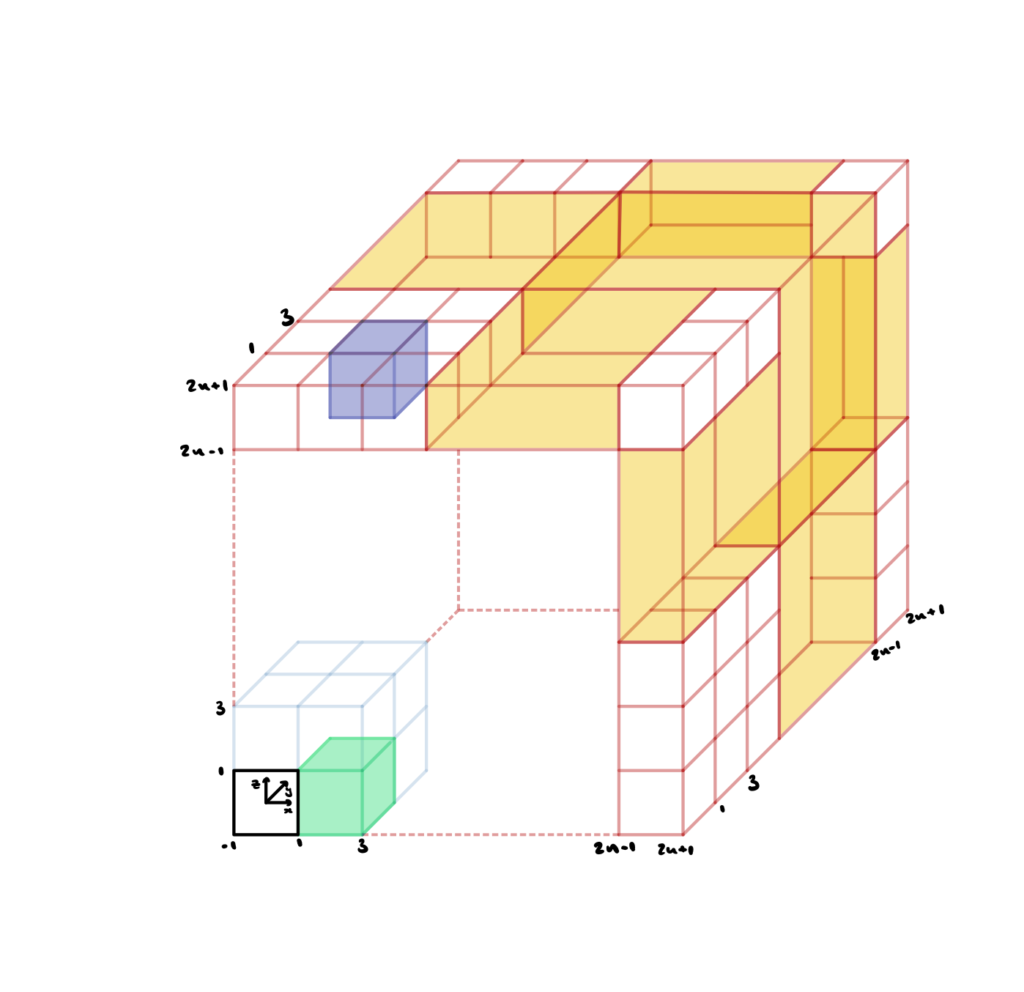
To copy the surface \(n^3\) times into the right grid cubes, we need find all the unique permutations of groups of three vectors chosen from \((0,2,4, \dots, 2n)\) and add them to the vertices matrix of the of the mesh. To update the face data, we add multiples of the number of vertices each time we duplicate into a new cube.
With this function in place, we can now see our triply periodic surfaces morphing as a larger structure.
Blender
A skill we continued developing and something we have grown to enjoy, is what we affectionately call “blendering.” To speak in technical terms, we use the open-source software Blender to generate triangle meshes that we, then, use as tests for our code.
For context: Blender is a free and open-source 3D computer graphics software tool set used for a plethora of purposes, such as creating animated films, 3D printed models, motion graphics, virtual reality, and computer games. It includes many features and it, truly, has endless possibilities. We used one small compartment of it: mesh creation and mesh editing, but we look forward to perhaps experiencing more of its possibilities in the future.
We seek to create shapes that are non-manifold; mathematically, this means that there exist local regions in our surface that are not homeomorphic to a subset of the Euclidean space. In other words, non-manifold shapes contain junctions where more than two faces meet at an edge, or more than two faces meet at a vertex without sharing an edge.
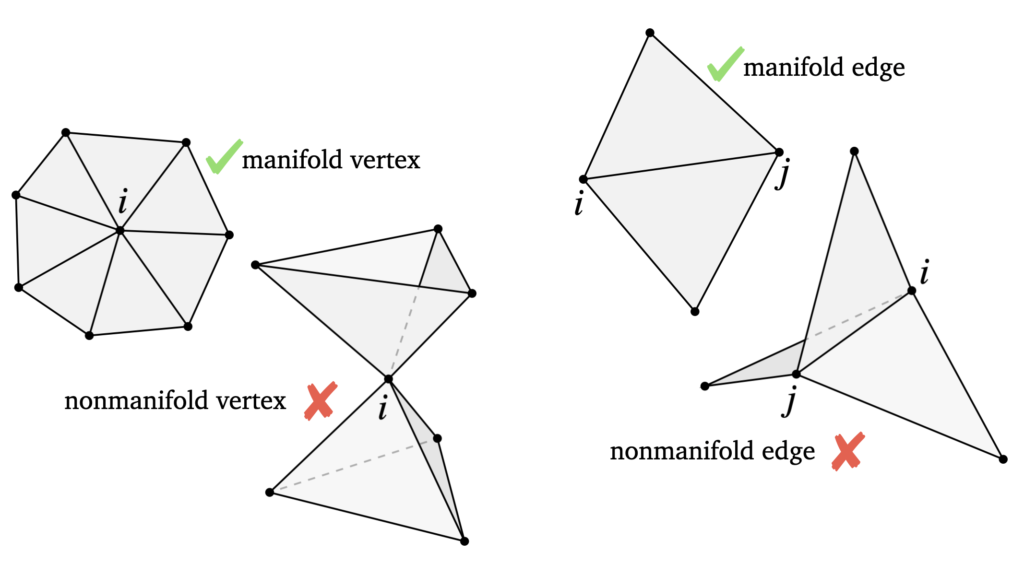
This is intellectually intriguing to consider, because most standard geometry processing methods and techniques do not consider this class of shapes. As such, most algorithms and ideas need to be redesigned for non-manifold surfaces.
Our Blender work consisted of a lot of trial-and-error. None of us had used Blender before, so the learning curve was steep. Yet, despite the occasional frustration, we persevered. With each hour worked, we increased our understanding and expertise, and in the end we were able to generate surfaces we were quite proud of. Most importantly, these triangle meshes have been valuable input for our algorithm and have helped us explore in more detail the differences between manifold and non-manifold surfaces.
Houdini
The new fellows joining this week came from a previous project on minimal surface led by Stephanie Wang, which used Houdini as a basis for generating minimal surfaces. Thus, we decided we could use Houdini to carry out some physical deformations, to see how non-manifold surfaces performed compared to similar manifold surfaces.
We used a standard Houdini vellum solver with some modifications to simulate a section of our surface falling under gravity. Below are some of the simulations we created.
Newton’s Method
When we were running Pinkhall and Polthier’s algorithm on our surfaces, we noticed that that algorithm would not stop at a local saddle point such as the Schwarz P surface, but would instead run until there was only a thin strip of area left, which is indeed a minimum, but not a very useful one.
Therefore, we switched to Newton’s Method to solve our optimization problem.
We define the triangle surface area as an energy: let the three vertices of a triangle be \(\mathbf{q}_1\), \(\mathbf{q}_2\), \(\mathbf{q}_3\). Then \(E = \frac{1}{2} \|\mathbf{n}\| \), where \(\mathbf{n} = (\mathbf{q}_2-\mathbf{q}_1) \times (\mathbf{q}_3-\mathbf{q}_1)\) is the surface area normal. Then we derive its Jacobian and Hessian, and construct the Jacobian and Hessian for all faces in the mesh.
However, this optimization scheme still did not converge to the desired minimum, perhaps because our initialization is far from the solution. Additionally, one of our project mentors implemented the approach in C++ and, similarly, no results ensued. Later, we tried to add line search to Newton’s Method, but also no luck.
Although our algorithm still does not converge to some minimal surfaces which we know to exist, it has generated the following fun bugs.
Future Work
In the previous blog post, we discussed studying the physical properties of nonmanifold TPMS. Over the past week, we used the Vellum Solver in Houdini and explored some of the differences in physical properties between manifold and nonmanifold surfaces. However, this is just the beginning — we can continue to expand our work in that direction.
Additional goals may include writing a script to generate many possible initial conditions, then converting the initial conditions into minimal surfaces, either by using the Pinkall and Polthier algorithm, or by implementing another minimal-surface-generating algorithm.
More work can be done on enumerating all of the possible nonmanifold structures that the Pinkall and Polthier algorithm generates. The researchers can, then, categorize the structures based on their geometric or physical properties. As mentioned last week, this is still an open problem.
Acknowledgments
We would like to thank our mentors Etienne Vouga, Nicholas Sharp, and Josh Vekhter for their patient guidance and the numerous hours they spent helping us debug our Matlab code, even when the answers were not immediately obvious to any of us. A special thanks goes to Stephanie Wang, who shared her Houdini expertise with us and, thus, made a lot of our visualizations possible. We would also like to thank our Teaching Assistant Erik Amezquita.