By Bryce Van Ross and Olga Guțan
Brief Existential Background
Most branches of geometry are viewed as either (1) subsets of pure mathematics or (2) disciplines derived from problems in engineering, architecture, and computational mathematics. But what is geometry itself?
Our work in the Summer Geometry Institute has been in the modern field of geometry processing. In this post, we will consider the philosophical aspects of geometry, and what they tell us about geometry processing specifically. The discussion has an inherent Eurocentric bias, and is, unfortunately, limited to Caucasian male philosophers.
The Roots of Geometry
In the eighteenth century, mathematics was primarily used to understand the natural sciences. For example, it was perceived as a language to better articulate physics, rather than as having intrinsic value. At that time, geometry was perceived as a form of applied mathematics. But where does the philosophy of geometry have its roots?
First we have Kant (1724-1804), who believed that our grasp of euclidean geometry must be instinctive. Opinions about this vary, based on each individual’s definitions of a priori knowledge and empiricism. Helmholtz, for example, agreed with Kant.
However, geometry processing incorporates not only euclidean geometry, but also calculus, linear algebra, differential equations, and topology. In addition, geometry processing includes a framework of algorithmic and optimization techniques. The knowledge of these topics varies from person to person, and therefore geometry processing can not be known a priori.
Back to the 18th century: as logical empiricism became popular, the progress of philosophy of geometry stalled. Geometry was reduced to a system of definitions and conventions; logic and mathematics were given priority. As a result, the last big wave of interest in the philosophy of geometry was in the 1920s — 100 years ago, and 116 years after Kant!
Space as a Mathematical Concept
Mathematical conclusions depend on the structure we confer to a space. The structure determines the permissible elements, as well as the operations that can be applied to the elements. Without imposing structure, it is difficult to impose “rules,” and the potency of math is, thus, diluted. Most spaces in euclidean geometry exist; in fact, they are embedded in the reality we live in. With other kinds of geometry, we must define the properties of the space first. Then, we can ask: what are the conditions for creating a space? What kinds of spaces, and therefore geometries, can we have? (Our personal favorite is the geometry of chance.)
Helmholtz (1821-1894) said the only allowable spaces are those that maintain constant curvature. This was eventually challenged by Einstein’s (1879-1955) Theory of Relativity. Weyl (1885-1955) came up with intuitive spaces, where it is possible to compare lengths only if two edges share the same spatio-temporal point. Similarly to the earlier-mentioned Kant (1724-1804), Carnap (1891-1970) claimed that intuition of spaces requires an n-dimensional topological space. As the philosophy of geometry evolved, so did our understanding of space.
“Waiting for Godot” in a Hyperbolic Space?
(The authors would like to gratefully acknowledge the primary source for the following sections.)
So what is geometry? Many people study it or use it… but what exactly are we interacting with?
As an exercise of imagination, consider being a two-dimensional (2D) entity in a 2D universe. In fact, you don’t even have to imagine, somebody already wrote about this. The book is, unfortunately, at times misogynistic, but the geometry is intriguing to consider. Back to the exercise of imagination: since everything in the 2D universe is finite, is the universe itself finite? A 2D mathematician might suggest that the universe looks like a rectangle. Does, then, the universe have a point beyond which travel is impossible? If so, it likely is different from all other points of the universe, by its construction, since it has a boundary. Imagine you are playing Asteroids. As you move your rocket ship towards the right — once it reaches the boundary, it will reappear on the left side. In mathematical language we say that “the left edge of the rectangle has been identified, point by point, with the right edge.”
How to Build a Torus When You Are Two-Dimensional
In three dimensions, we can glue these boundaries. First, we bend the rectangle to produce a cylinder, while being careful to glue only the left and right edges together. Since we are operating in a ‘perfect’ thought-based mathematical world, the cylinder is malleable. Now we bend it to achieve this second gluing, which looks like a donut. We call this a torus.
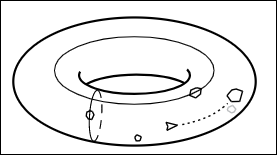
Recall that our reader currently lives in a 2D universe. A 2D person would not be able to see this torus in multiple dimensions. However, one would understand the space perfectly well, since the space can be identified back to the initial rectangle with edges. In this case, the universe is clearly finite, and with no edges.
Another surface with similar properties would be a two-dimensional sphere. A ladybug traveling on the sphere will notice that, locally, their world looks like a flat plane, and that the surface has no edges. On a small scale, if the mathematician ladybug splits the plane into triangles, the sum of the angles in each triangle will be 180 degrees. This is, in fact, known as a defining feature of euclidean geometry. However, on a larger scale, things start breaking.
A very large triangle drawn on the surface of the sphere has an angle sum far exceeding 180 degrees. Consider the triangle formed by the North Pole and two points on the equator of the sphere. The angle at each point on the equator is 90 degrees, so the total sum exceeds 180 degrees. Therefore, we conclude that — on a global scale — we can not apply euclidean geometry to a sphere. We call this hyperbolic geometry.

Shape and Connection
To conclude this exercise of imagination, we must say that there is a wonderful connection between the shape (topology) of a surface and the type of geometry it inherits. This relationship is given, mathematically, by the Gauss-Bonnet equation:
\(\kappa A = 2 \pi \xi\)
Where \(\kappa \) is the Gaussian curvature of a surface, A is the element of area of the surface, \(\pi \) is our good old friend 3.1415…, and \(\xi\) is the Euler characteristic of the surface. In other words, the “geometry” is on the left side of the equation and the “topology” is on the right side of the equation; and the equal sign shows how deeply connected they are.
Studying various shapes and how they connect is not only interesting, but also important. Particularly, if a two-dimensional entity can deduce what sort of global geometry reigns their immediate world, they may be able to deduce the possible shapes for the things in their larger universe.
To Really Conclude…
Although geometry processing has been around for a few decades, its philosophy is not yet well-studied. So far, this area shares themes with the broader philosophy of geometry, in certain topics:
- a priori vs empiricist knowledge,
- the evaluation of space and its elements,
- geometric human intuition,
- construction of geometries, and
- the study of shape and connection.
Given the computational aspect of geometry processing, there are additional important philosophical questions that arise, however they go beyond the scope of this post. It is difficult to determine whether such questions are best understood from the perspective of philosophy of geometry or philosophy of computer science, or both.
As geometry processing continues to impact our technological world, the philosophy of geometry processing will grow too. In the meantime, we should continue critically questioning our programming, our modeling, and — most importantly — the ethical implications of our work. We must also ensure that we have a functional understanding of the parts that constitute geometry processing. At the same time, it must be said that the discipline is more than just the sum of its parts.