By SGI Fellows Faria Huq, Sahra Yusuf and Berna Kabadayi
Over the first 2 weeks of SGI (July 26 – August 6, 2021), we have been working on the “Probabilistic Correspondence Synchronization using Functional Maps” project under the supervision of Nina Miolane and Tolga Birdal with TA Dena Bazazian. In this blog, we motivate and formulate our research questions and present our first results.
Finding a meaningful correspondence between two or more shapes is one of the most fundamental shape analysis tasks. Van Kaick et al (2010) stated the problem as follows: given input shapes \(S_1, S_2,…, S_N\), find a meaningful relation (or mapping) between their elements. Shape correspondence is a crucial building block of many computer vision and biomedical imaging algorithms, ranging from texture transfer in computer graphics to segmentation of anatomical structures in computational medicine. In the literature, shape correspondence has been also referred to as shape matching, shape registration, and shape alignment.
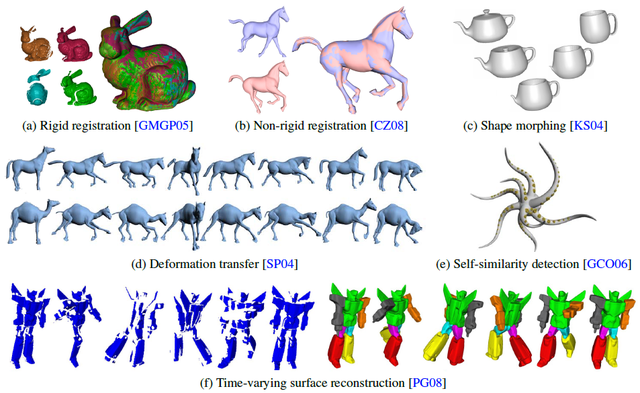
In this project, we consider a dataset of 3D shapes and represent the correspondence between any two shapes using the concept of “functional maps” [see section 1]. We then show how the technique of “synchronization” [see section 2] allows us to improve our computations of shape correspondences, i.e., allows us to refine some initial estimates of functional maps. During this project, we implement a method of synchronization using tools from geometric statistics and optimization on a Riemannian manifold describing functional maps, the Stiefel manifold, using the packages geomstats and pymanopt.
1. Representing Shape Correspondences with Functional Maps
Shape correspondence is a well-studied problem that applies to both rigid and non-rigid matching. In the rigid scenario, the transformation between two given 3D shapes can be described by a 3D rotation and a 3D translation. If there is a non-rigid transformation between the two 3D shapes, we can use point-to-point correspondences to model the shape matching. However, as mentioned in Ovsjanikov et al (2012), many practical situations make it either impossible or unnecessary to establish point-to-point correspondences between a pair of shapes, because of inherent shape ambiguities or because the user may only be interested in approximate alignment. To tackle that problem, functional maps are introduced in Ovsjanikov et al (2012) and can be considered a generalization of point-to-point correspondences.
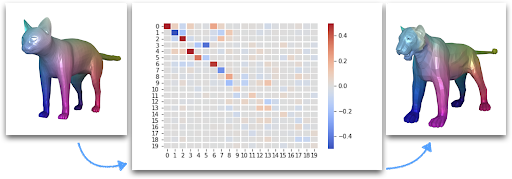
By definition, a functional map between two shapes is a map between functions defined on these shapes. A function defined on a shape assigns a value to each point of the shape and can be represented as a heatmap on the shape; see Figure 2 for functions defined on a cat and a tiger respectively. Then, the functional map of Figure 2 maps the function defined on the first shape — the cat — to a function on the second shape — the tiger. All in all, instead of computing correspondences between points on the shapes, functional maps compute mappings between functions defined on the shapes.
In practice, the functional map is represented by a \(p \times q\) matrix, called C. Specifically, we consider p basis functions defined on the source shape (e.g. the cat) and q basis functions defined on the target shape (e.g. the tiger). Typically, we can consider the eigenfunctions of the Laplace-Beltrami operator. The functional map C then represents how each of the p basis functions of the source shape is mapped onto the set of q basis functions of the target shape.
2. Problem Formulation: Synchronization Improves Shape Correspondences
In this section, we describe the technique of “synchronization” that allows us to improve the computations of functional maps between shapes, and we introduce the related notations. We use subsets of the TOSCA dataset (http://tosca.cs.technion.ac.il/book/resources_data.html), which contains a dataset of 3D shapes of cats, to illustrate the concepts.
Intuitively, the method of synchronization builds a graph that links pairs of 3D shapes within the input dataset by edges representing their functional maps; see Figure 3 for an example of such a graph with 4 shapes and 6 edges. The method of synchronization then leverages the property of cycle consistency within the graph. Cycle consistency is a concept that enforces a global agreement among the shape matchings in the graph, by distributing and minimizing the errors to the entire graph — so that not only pairwise relationships are modeled but also global ones. This is why, intuitively, synchronization allows us to refine the functional maps between pairs of shapes by extracting global information over the entire shape dataset.
Let’s now introduce notations to give the mathematical formulation of the synchronization method. We begin with a set of pairwise functional maps, \(C_{ij} \in \{\mathcal{F}(M_i,M_j)\}_{i,j}\) for \((i,j) \in \varepsilon\). M denotes the set of \(n\) input 3D shapes and \(\varepsilon\) denotes the set of the edges of the directed graph of \(n\) nodes representing the shapes: \(\varepsilon \subset \{1,\dots, n\} \times \{1,\dots, n\}\). We are then interested in finding the underlying “absolute functional maps” \(C_i\) for \(i\in\{1,\dots,n\}\) with respect to a common origin (e.g. \(C_0=I\), the identity matrix) that would respect the consistency of the underlying graph structure. We illustrate these notations in Figure 3. Given a graph of four cat shapes (cat8, cat3, cat9, cat4) and their relative functional maps (C83, C94, C34, C89, C48, C39), we want to find the absolute functional maps (C8, C3, C4, C9).

3. Riemannian Optimization Algorithm
In this section, we explain how we frame the synchronization problem as an optimization problem on a Riemannian manifold.
Constraints: As shown by Ovsjanikov et al (2012), functional maps are orthogonal matrices for near-isometry: the columns forming functional map matrix C are orthonormal vectors. Hence, functional maps naturally reside on the Stiefel manifold which is the manifold of matrices with orthonormal columns. The Stiefel manifold can be equipped with a Riemannian geometric structure that is implemented in the packages geomstats and pymanopt. We design a Riemannian optimization algorithm that iterates over the Stiefel manifold (or power manifold of Stiefels) using elementary operations of Riemannian geometry, and converges to our estimates of absolute functional maps. Later, we compare this method to the corresponding non-Riemannian optimization algorithm that does not constrain the iterates to belong to the Stiefel manifold.
Cost function: We describe here the cost function associated with the Riemannian optimization. We want our absolute functional maps to be consistent with the relative maps as much as possible. That is, in the ideal case, \(C_i \cdot C_{ij} = C_j \). To abide by this, we consider the following cost function in our algorithm:
\(\mathop{\mathrm{argmin}} _{{C_i \in \mathcal{F}}} \sum\limits_{(i,j)\in \varepsilon} {{\| C_i \cdot C_{ij} – C_j \|_F}^2 } \)
In this equation, we measure this norm in terms of the Frobenius norm, which is equal to the square root of the sum of the squares of the matrix values. This cost is implemented in Python, as follows:
# Cis are the maps we compute, input_Cijs are the input functional maps
def cost_function(Cis, input_Cijs):
cost = 0.
for edge, Cij in zip(EDGES, input_Cijs):
i, j = edge
Ci_Cij = np.matmul(Cis[i], Cij)
cost += np.linalg.norm(Ci_Cij - Cis[j], "fro") ** 2
return cost
Optimizer: Our goal is to minimize this cost with respect to the Cis, while constraining the Cis to remain on the Stiefel manifold. For solving our optimization problem, we use the TrustRegion algorithm from the Pymanopt library.
4. Experiments and Results
We present some preliminary results on the TOSCA dataset.
Dataset: For our baseline experiments, we use the 11 cat shapes from the TOSCA dataset. The cats have a wide variety of poses and deformations which make them particularly suitable for our baseline testing.
Initial Functional Map Generation: For each pair of cats within the TOSCA dataset, we compute initial functional maps using state-of-the-art methods, by adapting the source code from here. Our functional maps are of size 20 * 20, i.e they are written in terms of 20 basis functions on the source shape and 20 basis functions on the target shape.
Graph Generation: We implement a random graph generator using networkX that can generate cycle-consistent graphs. We use this graph generator to generate a graph, with nodes corresponding to shapes from a subset of the TOSCA dataset, and with edges depicting the correspondence relationship between the selected shapes. In our future experiments, this graph generator will allow us to compare the performance of our method depending on the number of shapes (or nodes) and the number of known initial correspondences (or initial functional maps) between the shapes (or sparsity of the graph).
Perturbation: We showcase the efficiency of our algorithm by inducing a synthetic perturbation on the initial functional maps and showing how synchronization allows us to correct it. Specifically, we add a Gaussian perturbation to the initial functional maps, with standard deviation s = 0.1, and project the resulting corrupted matrices on the Stiefel manifold to get “corrupted functional maps”. The corrupted functional maps are the inputs of our optimization algorithm.
Results: We demonstrate the result of our optimization algorithm for a subset of the TOSCA dataset and initial (corrupted) functional maps generated with the methods described above: we consider the graph with 4 shapes and 6 edges that was presented in Figure 3. The optimization algorithm converged in less than 20 iterations and less than 1 second. Figure 4 shows the output of our optimization algorithm on this graph. Specifically, we consider a function defined on one of the cats, and map it to the other cats using our functional maps. We can see how efficiently different body parts are being meaningfully mapped in each of these cat shapes.
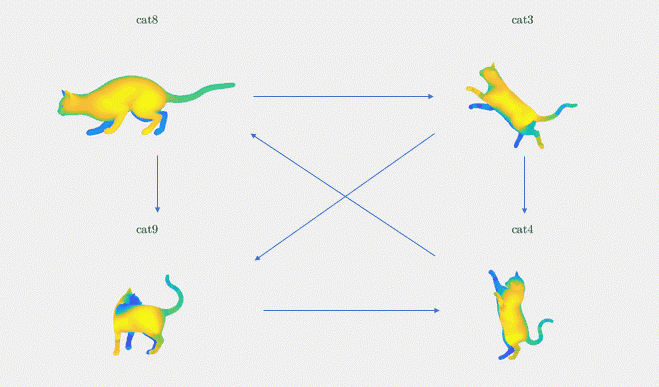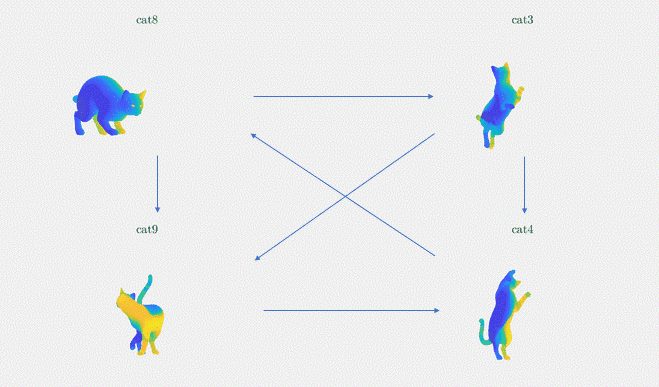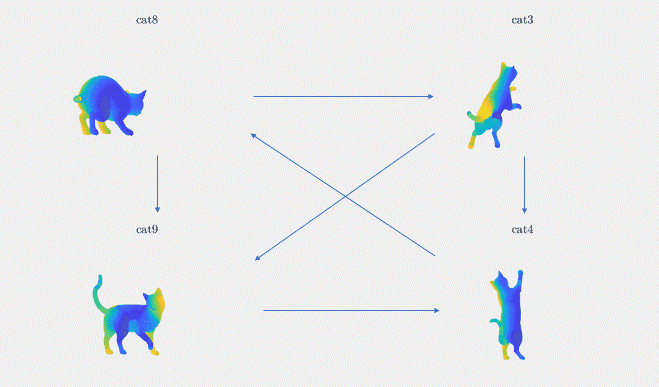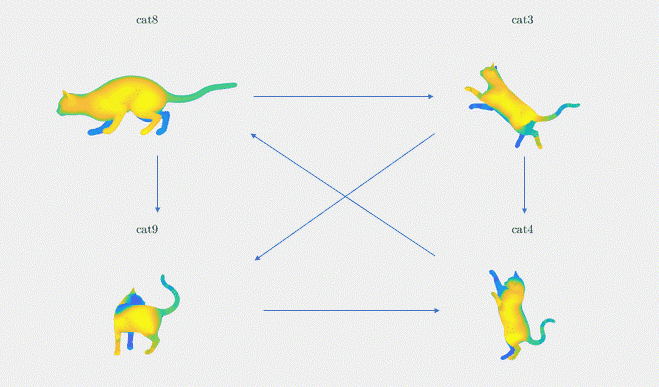
Figure 4. The absolute functional map output is visualized as point-to-point mapping, The regions marked with the same colors on the four shapes are being mapped to each other (noise standard deviation = 0.1)
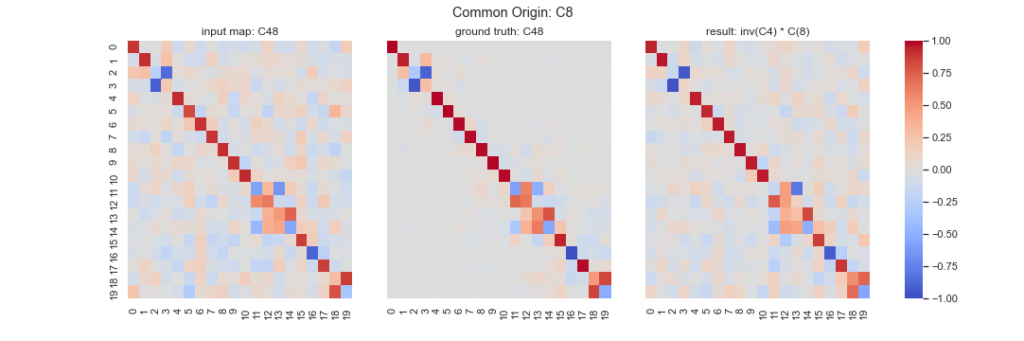
Comparison with initially corrupted functional maps: We show how synchronization allows us to improve over our initially corrupted functional maps. Figure 5 shows a comparison between the corrupted functional maps, the ground-truth (un-corrupted) functional maps, and the output functional maps computed via the output absolute maps given by our algorithm, for the correspondence between cat 4 and cat 8. While the algorithm does not allow to fully recover the ground-truth, our analysis shows that it has refined the initially corrupted functional maps. For example, we observe that the noise has been reduced for the off-diagonal elements. This visual inspection is confirmed quantitatively: the distance between the initially corrupted functional maps and the ground-truth is 2.033 while the distance between the output functional maps and the ground-truth is 1.853, as observed in Table 1.
However, the results on the other functional maps C83, C39, C94, C89, C34 are less convincing; see errors reported in Table 1. This can be explained by the fact that we have chosen a relatively small graph, with only 4 nodes i.e. 4 shapes. As a consequence, the synchronization method leveraging cycle consistency can be less efficient. Future results will investigate the performances of our approach for different graphs with different numbers of nodes and different numbers of edges (sparsity of the graph).
| Func. Maps. | Error C83 | Error C39 | Error C48 | Error C94 | Error C89 | Error C34 |
| Before sync. | 1.762 | 1.658 | 2.033 | 1.877 | 1.819 | 1.854 |
| After sync. | 1.659 | 2.519 | 1.741 | 2.323 | 2.118 | 2.492 |
| After sync. (Riem.) | 2.576 | 2.621 | 1.853 | 1.984 | 2.181 | 2.519 |
Discussion: We compare this method with the method that does not restrict the functional maps to be on the Riemannian Stiefel manifold. We observe similar performances, with a preference for the non-Riemannian optimization method. Future work will investigate which data regimes require optimization with Riemannian constraints and which regimes do not necessarily require it.
Conclusion
In this blog, we explained the first steps of our work on shape correspondences. Currently, we are working on a Markov Chain Monte Carlo (MCMC) implementation to get better results with associated uncertainty quantification. We are also working on a custom gradient function to get better performance. In the coming weeks, we look forward to experimenting with other benchmark datasets and comparing our results with baselines.
Acknowledgment: We thank our mentors, Dr. Nina Miolane and Dr. Tolga Birdal for their consistent guidance and mentorship. They have relentlessly supported us from the beginning, debugged our errors. We especially thank Nina for guiding us to write this blog post. We are very grateful for her keen enthusiasm 😇. We also thank our TA, Dr. Dena Bazazian for her important feedback.
Source code: See notebook here