By Tiago Fernandes, Anna Krokhine, Daniel Scrivener, and Qi Zhang
During the first week of SGI, our group worked with Professor Misha Kazhdan on a virtually omnipresent topic in the field of geometry processing: algorithmically assigning normal orientations to point clouds.
Introduction
While point clouds are the typical output of 3D scanning equipment, triangle meshes with connectivity information are often required to perform geometry processing techniques. In order to convert a point cloud to a triangle mesh, we first need to orient the point cloud — that is, assign normals \(\{n_1, … n_n\}\) and signs \(\{\alpha_1, … \alpha_n\}\) to the initially unoriented points \(\{p_1, … p_n\}\).
To find \(n_i\), we can locally fit a surface to each point \(p_i\) using its neighborhood \(N(i)\) and use its uniquely determined normal. More difficult, however, is the process of assigning consistent signs to the normals. In order to evaluate the consistency of the signs, we have the following energy function, which we minimize over alpha:
\(E(\alpha)=\alpha^T\cdot E\cdot \alpha\)
Where \(\alpha \in \{-1, +1\}^n\) is the vector of signs and \(\tilde{E}_{ij} = \begin{cases} \frac{\langle N_i(p_i), N_i(p_j)\rangle \cdot \langle N_j(p_i), N_j(p_j) \rangle}{2} & i \sim j \\ 0 & \text{otherwise}\end{cases}\).
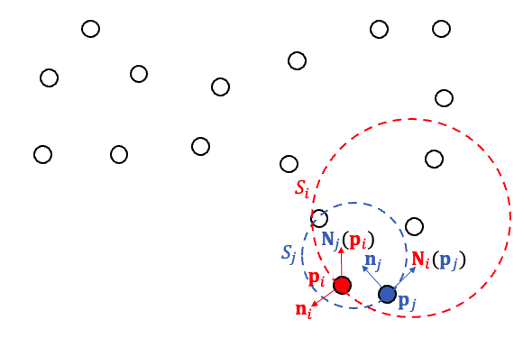
As shown in the diagram, \(N_i(p_j)\) is the normal assigned to \(p_j\) by the local surface fitted at \(p_i\). Greater values of \(E_{ij}\) indicate more consistent normal orientations, and thus we encourage neighboring points to have similar orientations.
Our goal is to obtain a set of signs minimizing this energy function, which is difficult to calculate on the full point set at once. To simplify the process, we looked at algorithms built on a hierarchical approach: we solve the problem first on small clusters of points, recursively building larger solutions until we’ve arrived at the initial problem.
Within this general algorithmic structure, we explored different possibilities as to the surfaces used to represent each cluster of points locally. Prof. Kazhdan had previously tried two approaches, one linear and the other quadratic. The linear approach assigns best-fit planes to the neighborhood around each point, whereas the quadratic approach uses general quadratic functions of best fit.
While these techniques provided a good foundation, we identified several failure cases upon experimenting with various point clouds. The linear approach works well on simple faces, but struggles to maintain consistent orientation around sharp features like edges. This is best demonstrated with the flower pointset, where the orientations of the normals are inverted in some clusters. The quadratic approach does better with fitting to distinctive features but overfits to what should be more simple surfaces, producing some undesirable outcomes such as the flower and vase seen below.

Defining New Fits: First Attempt
Given that the linear and quadratic fits presented their own unique shortcomings, it became clear that we needed to experiment with different surface representations in order to find suitable fits for all clusters. Thanks to the abstract nature of our framework, there were few limitations on how the implicit surface needed to be defined; the energy function requires only a method for querying the gradient as well as a means of flipping the gradient’s sign, which leaves many options for implementation.
Our first geometric candidate was the sphere, a shape that approximates corners well due to the fact that it has curvature in all three directions. Additionally, fitting a set of points to a sphere is fairly straightforward: we used the least-squares approach described here, which, in implementation terms, is no more difficult than setting up a linear system and solving it. Unfortunately, the simplest solutions are not always the best solutions…

The spherical fitting wasn’t able to deal with sharp edges as expected, incorrectly matching the normal orientations when merging clusters close to those edges. It also generated some noise across the surface. But the process of designing the spherical fit gave us a solid idea on how to model other surfaces (and also helped to demystify some esoteric C++ conventions).
Parabolic Fit
We’ve established that since the surface may curve, a linear fit can be non-faithful to the features of the original pointset. Conversely, the generic quadratic fit has the potential to produce undesirable surface representations such as hyperbolas or ellipsoids. To this end, we introduced a parabolic fit, which improves upon the linear fit via the addition of a parameter.
By constructing a local coordinate frame where the normal from the linear fit serves as our z-axis, we were able to fit \(z=a(x^2 + y^2)\) with energy \(E_{loss} = \sum\limits_{i} (z_i – a(x_i^2+y_i^2))^2\). From this we obtained \(a = \frac{\sum_i z_i (x_i^2+y_i^2 ) }{\sum_i(x_i^2+y_i^2 )^2}\) yielding an \(a\) that minimizes this energy. By observing that \(z_i=\langle \vec{p_0 p_i} ,n \rangle, x_i^2+y_i^2=||\vec {p_0 p_i} \times n||^2\) , we derived a formula that is easier to represent programmatically: \(a = \frac{\sum_i \langle \vec{p_0 p_i} ,n \rangle ||\vec {p_0 p_i} \times n||^2 }{\sum_i||\vec {p_0 p_i} \times n||^4}\).
We calculated the gradient in a similar manner. Since locally \(\nabla ( z – a(x^2+y^2)) = (-2ax,-2ay,1) = -2a(x,y,0) + (0,0,1)\), then \(\nabla ( z – a(x^2+y^2)) = -2a\cdot \mbox{Proj}(\vec{p_0 p_i}) + \vec{n}\), where \(\mbox{Proj}( )\) projects vectors into the plane obtained in the original fit, which is written in a more code-friendly manner as \(\mbox{Proj}(\vec{x}) = \vec{x} – \langle \vec{x}, \vec{n} \rangle \vec{n}\). Finally, the gradient could be expressed as \(\nabla ( z – a(x^2+y^2)) = -2a(\vec{x} – \langle \vec{x}, \vec{n} \rangle \vec{n}) + \vec{n}\).
Our implementation of the parabolic fit generally works better than the linear fit, correcting for some key errors. It works particularly well on smooth, curved point clouds.
As for the flower dataset, however, the performance was still sub-par. When we examined some of the parabolic fits using a tool to visualize the isosurface, we found the following problem with some of the normals:
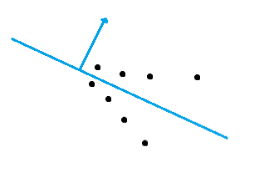
In this example, \(\vec{p_0 \bar p}\) would serve as a better normal vector than \(\vec{n}\), so we decided to implement a “choice” between the two. To avoid swapping the normal on flat point clouds (where the original normal serves its purpose quite well) we determined a threshold to handle this. Intuitively, a point cloud encoding an edge will yield a larger \(||\vec{p_0 \bar p}||\):
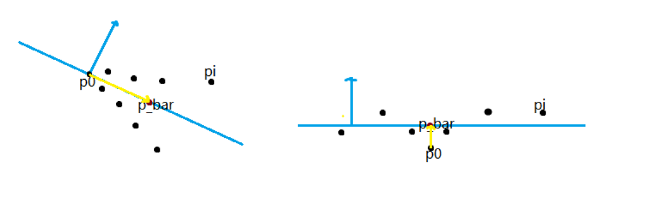
To obtain a good threshold value, we used the local radius \(d_{max} = \max _{i} ||\vec{p_0 p_i}||\) and then picked a $ c$ that seems to work with our dataset (related to the size of each neighborhood), such that when \(||\vec{p_0 \bar p}|| < d_{max}/c\), we can assume the cluster is flat, whereas when \(||\vec{p_0 \bar p}||\ge d_{max}/c\) we expect it to be sharp.

In practice, this idea works well on flower.xyz when \(c \ge 12\) — the parameter is rather sensitive and can yield poor results on some point clouds if not tuned properly.
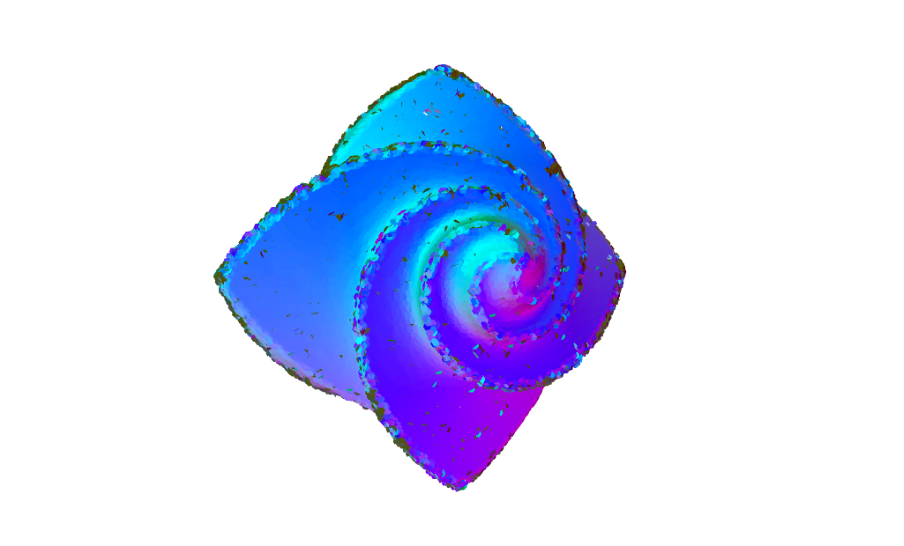
Hybrid Methods: The Associative Fit
The parabolic fit provided a lot of hope as to how we could definitively address large variations in curvature. Recalling that the quadratic fit worked well for some types of clusters and that the linear fit worked well for others, the advantages of somehow being able to merge the two methods by leveraging both of their strengths had become apparent. This observation is what ultimately gave rise to the “associative” fit, which
- constructs two different fits for each cluster, and
- chooses the best fit by comparing the performance of the first fit to a user-specified threshold value.
The first fit’s performance is assessed according to a standard statistical measurement known as R-squared, which tells us, as a percentage, how much of the point cluster’s variation is explained by the chosen fit (or simply put, the correlation between the fit and the pointset). This was straightforward enough to implement with respect to our linear fit, which always serves as the first fit that AssociativeFit attempts to query. We can completely disable the linear fit when its R-squared value does not meet the threshold for inclusion, allowing us to switch to a better fit (quadratic, parabolic) for clusters where the observed variance is too great for a planar representation. As it turns out, clusters with high variance are likely to encode geometries with high curvature, which makes the use of a higher-degree fit appropriate.
Many of our best results were obtained using the associative fit, and we were pleased to see clear improvements over the original single-fit approaches. The inclusion of a threshold parameter does necessitate a lot of hands-on trial and error by the user — we’d eventually like to see this value determined automatically per-pointset, but the optimization problem involved in doing so is particularly challenging given that each point cloud has its own issues related to non-uniform sampling and density.

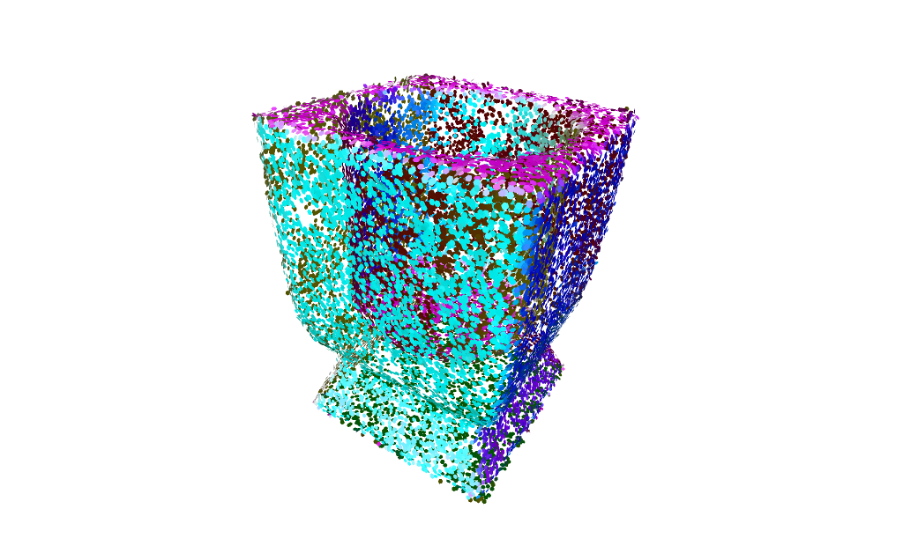
Quantitative Performance, Distance Weighting, and Other Touch-Ups
Aside from defining new implicit surfaces, we made a lot of other miscellaneous changes to the existing code base in order to improve our means of assessing each fit’s performance. We also wanted to provide the user with as much flexibility as possible when it came to manual refinement of the results.
At the beginning, when it came time to analyze our results, we relied heavily upon the disk-based visualization tool used to generate the images in this blog post. We also explored geometry processing techniques (mainly Poisson reconstruction) that make extensive use of the generated normals, assessing their performance as a proxy for the success of our method. These tools, however, provide only a qualitative means of assessment, essentially boiling down to whether a result “looks good.”
Fortunately, many of the point clouds in our dataset came with pre-assigned “true” normals that were then discarded by our method as it attempted to reconstruct them. We could easily use these normals as a point of comparison, allowing us to generate two metrics: similarity of normal lines (absolute value of the dot product, orientation-agnostic) and similarity of orientations (sign of the dot product). These statistics not only helped us with our debugging, but serve as natural candidates for any future optimization process that compares multiple passes of the algorithm.
The last main improvement to cover is the introduction of “weights” in the construction of each fit, or attenuating values that attempt to diminish the contribution of points farthest away from the mean. Despite having been implemented before we even touched the codebase, the weights were not used until we enabled them (previously, each fit received a weighting function that always returned a constant value rather than one of these distance-based weights). Improvements were modest in some cases and quite noticeable in others, as indicated by our results.


Conclusion
The problem of orienting point clouds is NP-hard in its simplest formulation, and a good approach for this task needs to take advantage of the geometric properties and structure of point clouds. By implementing more complex surface representations, we were able to significantly improve the results obtained across the 17 point clouds used for testing. The associative & parabolic fits in particular produced promising results: both were able to preserve the orientations of clusters across sharp edges and smooth surfaces alike.
Several obstacles remain with regard to our approach. The algorithm may perform poorly on especially dense point clouds or point clouds with non-manifold geometry. Additionally, our new surface representations are sensitive to manually-specified parameters, preventing this method from working automatically. Fortunately, the latter issue presents an opportunity for future work with optimization.
It was exciting to start off SGI working on a project with so many different applications in the field of geometry processing and beyond. The merit of this approach lies primarily with the fact that it provides an out-of-the box solution: once you compile the code, you can start experimenting with it right away (there are no neural networks to train, for example). We’re hopeful that this work will only continue to see improvements as adjustments are made to the various surface implementations (and there may be a part II on that front — stay tuned!)