Author: sergius.justus

Mentor:Dr. Karthik Gopinath

Volunteer Mentor: Kyle Onghai.

Fellows: Sergius Justus Nyah, Nicolas Pigadas, Mutiraj Laksanawisit

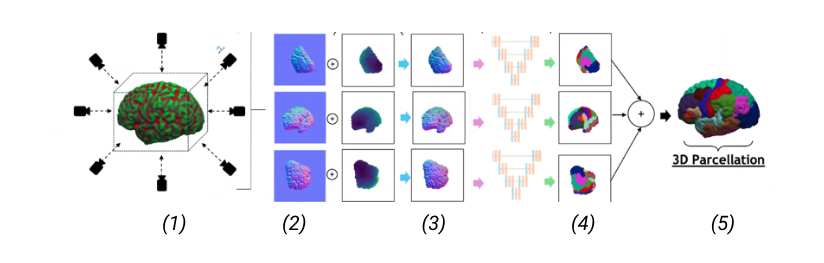
Picture 1: A high-level of the 2D projection descriptor pipeline we propose. (1) Extraction of multiple views and multiple descriptors from the 3D shape; (2) The extracted descriptors can be: normals, depth and curvature; (3) Input of the descriptors into a multi-view network; (4) Segmentation of the views (5) 3D reconstruction of the 3D segmented shape.

Abstract

Labeling brain surfaces is vital to many aspects of neuroscience and medicine, but to do so manually is laborious and time-consuming.  An automated method would streamline the process, enabling more efficient analysis and interpretation of neuroimaging data. Such a task aligns with the longstanding inquiry in computer vision: is it more effective to use 3D shape representations or would 2D projection descriptor approaches yield better understanding of the shape? In this work, we explore the 2D approach of this question. We propose an automated end-to-end pipeline, structured into four main phases: selection of views for 2D projection extraction, rendering of the cortical mesh from multiple perspectives, segmentation of these projections and inverse rendering to map 2D segmentations back to 3D, integrating multiple views (Picture 1)

Definitions of Basic Project-Related Terms:

• Pseudo-Rendering:  This is a process whereby a 3D model, such as a cortical mesh (in our case), is projected into 2D images from multiple perspectives. This process involves a transformation from the 3D coordinate space to the 2D image plane. The perspectives can be defined by a virtual camera’s position and orientation relative to the 3D model. The resulting 2D images retain depth information from the 3D model, hence bringing forth the perception of three-dimensionality.

• 2D Segmentation: 2D Segmentation is the process of dividing a 2D image into distinct regions based on pixel characteristics such as color, intensity, or texture. The segmentation method, which can include techniques like thresholding, clustering, watershed, and edge-based methods, determines how these regions are defined. For example, in an image of an airplane in the sky, one region might be the blue sky and another the white airplane. Similarly, an image of a chair could be segmented into regions representing the chair’s legs, seat, and backrest. Post-processing steps may be applied to refine these regions. The success of the segmentation can be evaluated using metrics like pixel accuracy, Intersection over Union (IoU), and Dice coefficient (a measure of the performance of Segmentation algorithms).

• Cortical Mesh: This is a 3D model that represents the outer surface of the brain (cerebral cortex), usually obtained from Magnetic Resonance Imaging data.

• Parcellation: This refers to the process of dividing cortical meshes, typically derived from brain imaging data, into distinct regions or parcels. These parcels often represent functionally or structurally distinct areas of the brain. Its purpose here is to simplify the analysis of brain imaging data by reducing the complexity of the data and focusing on regions of interest.
  

Initial Steps:

1. Load and visualize Brain surfaces with FreeSurfer [Link] 
2. Compute Normals, Curvature, and Point clouds from the Mesh surface

Method:

Selecting camera views to Extract 2D Images.

The selection of camera views is a critical step which involves determining the optimal perspectives from which to project the 3D cortical mesh onto 2D planes. Our goal here is to capture the most informative views that will facilitate accurate segmentation and subsequent inverse rendering.

We will start adopting a systematic approach to select six canonical views: Front, Bottom, Top, Right, Back, and Left. These views are chosen to ensure comprehensive coverage of the cortical surface, capturing its intricate geometry from multiple angles.

The selection process begins by computing the intrinsic matrix for the camera, which is used to simulate the camera’s perspective. The intrinsic matrix is calculated using the following function in Python:

def compute_intmat(img_width, img_height):

    intmat = np.eye(3)

    # Fill the diagonal elements with appropriate values
    np.fill_diagonal(intmat, [-(img_width + img_height) / 1, -(img_width + img_height) / 1, 1])

    # Set the last column of the matrix for image centering
    intmat[:,-1] = [img_width / 2, img_height / 2, 1]

    return intmat

Next, we’ll create external transformation matrices to align the camera with the six predefined views. These matrices help us generate rays for ray casting, allowing us to simulate what the camera would see from each perspective. We’ll use the pinhole camera model to generate these rays.

def generate_maps(mesh, labels, intmat, extmat, img_width, img_height, rotation_matrices, recompute_normals):
    assert isinstance(mesh, o3d.t.geometry.TriangleMesh)
    assert isinstance(labels, np.ndarray) and labels.shape == (mesh.vertex.normals.shape[0],)
    assert isinstance(intmat, np.ndarray) and intmat.shape == (3, 3)
    assert isinstance(extmat, np.ndarray) and (extmat.shape == (1, 4, 4) or extmat.shape == (6, 4, 4))
    assert isinstance(img_width, int) and img_width > 0
    assert isinstance(img_height, int) and img_height > 0

    if recompute_normals:
        mesh.vertex.normals = mesh.vertex.normals@np.transpose(rotation_matrices[0][:3,:3].astype(np.float32))
        mesh.triangle.normals = mesh.triangle.normals@np.transpose(rotation_matrices[0][:3,:3].astype(np.float32))

    scene = o3d.t.geometry.RaycastingScene()
    scene.add_triangles(mesh)

    output_maps, labels_maps, ids_maps, vertex_maps = [], [], [], []

    for i in range(rotation_matrices.shape[0]):
        rays = scene.create_rays_pinhole(intmat, extmat[i], img_width, img_height)
        cast = scene.cast_rays(rays)
        ids_map = np.array(cast['primitive_ids'].numpy(), dtype=np.int32)
        ids_maps.append(ids_map)
        hit_map = np.array(cast['t_hit'].numpy(), dtype=np.float32)
        weights_map = np.array(cast['primitive_uvs'].numpy(), dtype=np.float32)
        label_ids = np.argmax(np.concatenate((weights_map, 1 - np.sum(weights_map, axis=2, keepdims=True)), axis=2), axis=2)

        normal_map = np.array(mesh.triangle.normals[ids_map.clip(0)].numpy(), dtype=np.float32)
        normal_map[ids_map == -1] = [0, 0, -1]
        normal_map[:, :, -1] = -normal_map[:, :, -1].clip(-1, 0)
        normal_map = normal_map * 0.5 + 0.5

        vertex_map = np.array(mesh.triangle.indices[ids_map.clip(0)].numpy(), dtype=np.int32)
        vertex_map[ids_map == -1] = [-1]
        vertex_maps.append(vertex_map)

        inverse_distance_map = 1 / hit_map
        coded_map_inv = normal_map * inverse_distance_map[:, :, None]
        output_map = (coded_map_inv - np.min(coded_map_inv)) / (np.max(coded_map_inv) - np.min(coded_map_inv))
        output_maps.append(output_map)

        labels_map = labels[vertex_map.clip(0)]
        labels_map[vertex_map == -1] = -1
        labels_map = labels_map[np.arange(labels_map.shape[0])[:, np.newaxis], np.arange(labels_map.shape[1]), label_ids]
        labels_map = labels_map.astype('float64')
        labels_maps.append(labels_map)

    return np.array(output_maps), np.array(labels_maps)

By casting rays from these six perspectives, we can project the entire cortical surface onto 2D planes, making sure we capture all the important features. This multi-view approach strengthens the segmentation process by reducing the chances of occlusions and giving us a more complete picture of the 3D structure.

The following images illustrate the six canonical views we used in our pipeline:

Now, We will accompany each 2D projection with annotations (ground truth).

These views are crucial for the next steps in our pipeline, such as rendering, segmentation, and inverse rendering. By carefully choosing and using these perspectives, we improve both the accuracy and efficiency of the automated labeling process. The six camera positions ensure that every part of the cortical surface is captured, giving us a complete set of 2D projections that can be accurately mapped back to the 3D structure.

2D Projections: Annotations and Curvature

To continue, we take the 2D projections obtained from the six camera views and perform annotations and curvature calculations, which are essential for understanding the cortical surface’s geometry and features.

Process:

1. Calculate the curvature of the cortical surface from the 2D projections, which helps in identifying important features and understanding the surface’s geometry.
2. Annotate the 2D projections with relevant labels, such as different brain regions or anatomical landmarks.
3. Use these annotations to the CNN (As seen below) for automated labeling.

Code:

# Compute per-face curvature using gpytoolbox (angle defect)
curvature = gpy.angle_defect(vertices, faces)


# Debugging: Print raw curvature values
print("Raw Curvature Values:")
print(curvature)
print("Curvature min:", np.min(curvature))
print("Curvature max:", np.max(curvature))


# Percentile-based normalization
lower_percentile = np.percentile(curvature, 1)
upper_percentile = np.percentile(curvature, 99)


# Clipping the curvature values to the 1st and 99th percentiles to diminish the effect of outliers
curvature_clipped = np.clip(curvature, lower_percentile, upper_percentile)


# Normalize the clipped curvature values between 0 and 1
curvature_normalized = (curvature_clipped - lower_percentile) / (upper_percentile - lower_percentile)


# Debugging: Print normalized curvature values
print("Normalized Curvature Values:")
print(curvature_normalized)


# Select color map
color_map = plt.get_cmap('viridis')
curvature_colors = color_map(curvature_normalized)[:, :3] # Ignore alpha channel


# Create Open3D mesh
mesh = o3d.geometry.TriangleMesh()
mesh.vertices = o3d.utility.Vector3dVector(vertices)
mesh.triangles = o3d.utility.Vector3iVector(faces)
mesh.vertex_colors = o3d.utility.Vector3dVector(curvature_colors) # Apply colors to vertices


# Compute normals to improve lighting in visualization
mesh.compute_vertex_normals()


# Visualize the mesh with curvature coloring
o3d.visualization.draw_geometries([mesh], window_name='Mesh with Curvature Colors')


# Visualize the normalized curvature values as a histogram
plt.figure()
plt.hist(curvature_normalized, bins=50, color='blue', alpha=0.7)
plt.title("Histogram of Normalized Curvature Values")
plt.xlabel("Normalized Curvature")
plt.ylabel("Frequency")
plt.show()

Result (As seen also in (2) above):

Training the multi-view CNN

Now we use the annotated 2D projections to train a multi-view Convolutional Neural Network (CNN). This multi-view CNN leverages the different perspectives to improve the accuracy of the labeling process.

Process:

1. Data Preparation:
   • Prepare the annotated 2D projections as input data for the CNN.
   • Split the data into training, validation, and test sets.

import os
import nibabel as nib
import torch
from torch.utils.data import Dataset, DataLoader

def load_data(data_dir):

    data = []
    labels = []

    for subject_dir in os.listdir(data_dir):
        surf_dir = os.path.join(data_dir, subject_dir, 'surf')
        label_dir = os.path.join(data_dir, subject_dir, 'label')

        if os.path.isdir(surf_dir) and os.path.isdir(label_dir):
            # Load surface data
            surf_file = os.path.join(surf_dir, 'lh_aligned.surf')
            if os.path.exists(surf_file):
                surf_data = nib.freesurfer.read_geometry(surf_file)[0]
                data.append(surf_data)

            # Load label data
            label_file = os.path.join(label_dir, 'lh.annot')
            if os.path.exists(label_file):
                label_data = nib.freesurfer.read_annot(label_file)[0]
                labels.append(label_data)

    return np.array(data), np.array(labels)


# Load actual data
train_data, train_labels = load_data('/home/sergy/cortical-mesh-parcellation/10brainsurfaces (1)')
val_data, val_labels = load_data('/home/sergy/cortical-mesh-parcellation/10brainsurfaces (1)')


# Convert data to PyTorch tensors
train_data = torch.tensor(train_data, dtype=torch.float32)
train_labels = torch.tensor(train_labels, dtype=torch.long)
val_data = torch.tensor(val_data, dtype=torch.float32)
val_labels = torch.tensor(val_labels, dtype=torch.long)


# Define custom dataset class
class ExampleDataset(Dataset):
    def __init__(self, data, labels):
        self.data = data
        self.labels = labels

    def __len__(self):
        return len(self.data)

    def __getitem__(self, index):
        return self.data[index], self.labels[index]


# Create DataLoader for training and validation data
train_dataset = ExampleDataset(train_data, train_labels)
val_dataset = ExampleDataset(val_data, val_labels)

train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)

2. Model Architecture:

• Design a CNN architecture that can handle multi-view inputs.
• Use techniques like data augmentation to improve the model’s robustness.

from trainCNN import MultiViewCNN
import torch.nn as nn

# Initialize the model
model = MultiViewCNN()

# Define the loss function and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

3. Training the CNN:

• Train the CNN using the prepared data.
• Monitor the training process using metrics like accuracy and loss.

# Training loop
for epoch in range(5):  # 5 epochs
    model.train()
    for i, (inputs, labels) in enumerate(train_loader):
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        if i % 100 == 0:
            print(f"Epoch [{epoch+1}/5], Step [{i+1}/{len(train_loader)}], Loss: {loss.item():.4f}")

    # Validation loop
    model.eval()
    val_loss = 0.0
    with torch.no_grad():
        for inputs, labels in val_loader:
            outputs = model(inputs)
            loss = criterion(outputs, labels)
            val_loss += loss.item()

    val_loss /= len(val_loader)
    print(f"Validation Loss after Epoch [{epoch+1}/5]: {val_loss:.4f}")

Training result:

Analysis of Training Results:

Initial Loss: In the first epoch, the initial loss is 2.3174. This indicates that the model is starting to learn from the data, but there is still a significant difference between the predicted and actual labels.

Subsequent Epochs: From the second epoch onwards, the loss drops to 0.0000. This suggests that the model has quickly learned to minimize the loss and make accurate predictions.

3D Reconstruction: Annotations and Curvature: 

To conclude, we will map the 2D annotations and curvature back to the 3D structure, which provides a comprehensive view of the cortical surface with detailed annotations and curvature information. We can divide this into 3 steps;

1. Mapping Annotations:

Firstly, we will map the annotations predicted by the Multi-View CNN back to the 3D cortical surface, which involves projecting the 2D annotations onto the 3D mesh.

import numpy as np
def map_annotations_to_3d(annotations_2d, vertices, faces):
    # Initialize a 3D array to store the annotations
    annotations_3d = np.zeros(vertices.shape[0])
    # Iterate over each face and map the 2D annotations to the 3D vertices
    for i, face in enumerate(faces):
        for vertex in face:
            annotations_3d[vertex] = annotations_2d[i]
    return annotations_3d
# Example usage
annotations_2d = np.random.randint(0, 10, size=(faces.shape[0],))  # Replace with actual 2D annotations
annotations_3d = map_annotations_to_3d(annotations_2d, vertices, faces)

2. Mapping Curvature:

We then map the calculated curvature values from the 2D projections back to the 3D surface. This will help us in visualizing the curvature on the 3D model.

def map_curvature_to_3d(curvature_2d, vertices, faces):
    # Initialize a 3D array to store the curvature values
    curvature_3d = np.zeros(vertices.shape[0])
    
    # Iterate over each face and map the 2D curvature to the 3D vertices
    for i, face in enumerate(faces):
        for vertex in face:
            curvature_3d[vertex] = curvature_2d[i]
    
    return curvature_3d

# Define vertices and faces
vertices = np.array([[0, 0, 0], [1, 0, 0], [1, 1, 0], [0, 1, 0]])
faces = np.array([[0, 1, 2], [0, 2, 3]])

3.  Integration and Visualization:

Finally, we will integrate the annotations and curvature into a single 3D model and use a visualization tool (Polyscope, in this case) to display the final annotated and curved 3D structure.

# Load annotations and curvature data
annotations_path = '10brainsurfaces (1)/100206/label/lh.annot'
curvature_path = 'curvature_array.npy'
annotations_3d = nib.freesurfer.read_annot(annotations_path)[0]
curvature_3d = np.load(curvature_path)
# Ensure curvature_3d has the correct shape
if curvature_3d.shape[0] != vertices.shape[0]:
    curvature_3d = curvature_3d[:vertices.shape[0]]
# Initialize Polyscope
ps.init()

# Register the 3D mesh with Polyscope
mesh = ps.register_surface_mesh("annotated_brain", vertices, faces)
# Add the annotations and curvature as scalar quantities
mesh.add_scalar_quantity("annotations", annotations_3d, defined_on="vertices", cmap="viridis")
mesh.add_scalar_quantity("curvature", curvature_3d, defined_on="vertices", cmap="coolwarm")
# Show the visualization
ps.show()

Final Results from Annotations and Mappings:

Our pipeline successfully achieved its goals:

• The trainCNN script trained the MultiViewCNN model and saved the state dictionary.
• The projections.py script visualized the cortical mesh with annotations and curvature, as seen below
• The trained model extracted features from the 2D projections, enhancing our understanding of the cortical surface.
• Our goal of Pseudo Rendering was achieved.

Figure 1: Front view of brain section with labeled annotations:

Figure 2: Back view of brain section with labeled annotations:

To conclude this long post, permit us discuss the practical use-scopes of Pseudo rendering, across diverse feilds in Science, healthcare, and Research:

• Pseudo-rendering enhances the visualization of complex anatomical structures, aiding in better diagnosis and treatment planning by providing detailed 3D models of organs and tissues.
• Enables efficient analysis of 3D data by generating 2D projections from multiple camera angles, like in the case of cortical mesh parcellation.
• Reduces computational resources required for rendering complex 3D models, making the process less resource-intensive.
• Supports interactive exploration of 3D models, allowing users to manipulate 2D projections to explore different views and perspectives.

Closing Remarks:

At this point, we would like to express our gratitude to our amazing mentor, Dr. Karthik Gopinath, and volunteer mentor, Kyle Onghai, for their unwavering support and guidance throughout the project. Their effective guidance enabled us to rapidly develop our ideas and foster a deep passion for the project. We look forward to continuing our work on this brilliant research idea as soon as possible.

Thank you for reading this far! 🎉

Long Live the SGI!

A cool aspect of the SGI is the opportunity to engage with distinguished guest speakers ranging from both industry and academia who deliver captivating talks on topics centered around Geometry Processing. On August 8th, we had the pleasure of hearing from Professor Lining Yao, the director of the Morphing Matter Lab at the University of California Berkeley. Her talk was a captivating journey into the world of morphing materials and their potential impact on sustainable design.

The Intersection of Design and Sustainability

Professor Yao kicked off her talk by discussing her research focus on “morphing materials” — materials that can change properties and shapes in response to environmental stimuli. She emphasized the importance of combining human-centered design with nature-centered principles, a dual approach which aims to create products that not only benefit people but also minimize harm to the environment.

Real-World Applications of Morphing Materials

One of the examples Prof. Yao shared was a biodegradable material inspired by the seed of Erodium. This innovative design allows the seed to bury itself into the ground after rain, which enhances its germination rate. This, probably, is a fantastic example of how nature can inspire sustainable technology. She further explained that such self-burying seeds could be used for ecological restoration, which makes them a powerful tool for environmental conservation.

Figure 1: A photo of a seed of Erodium, a genus of plants with seeds that unwind coiled tails to act as a drill to plant into the ground.

Photo credits: Morphing Matter Lab – CMU

Another fascinating application of Morphing Materials is in the realm of 4D printing (an advanced form of 3D printing that incorporates the dimension of time into the manufacturing process, enabling printed objects to change shape or function over time in response to environmental stimuli such as heat, moisture, light, or other factors). Prof. Lining described how self-folding structures could revolutionize manufacturing by reducing material waste and production time. For instance, a flat sheet could be printed and then transformed into a chair, saving both resources and energy.

This short video shows a demonstration 4D printing of Self-folding materials and interfaces.

Source: Morphing Matter Lab

The fun side of Morphing Materials

Professor Lining didn’t stop at serious applications; she also introduced us to the fun and playful side of her research work. Imagine Italian pasta that can morph from a flat shape into various delicious forms when cooked! This innovative approach not only saves packaging space during transportation and storage, but also contributes to reducing plastic waste. This tells us that sustainability can be both functional and fun.

The Video below demonstrates a Flatpack of morphing pasta for sustainable food packaging and greener cooking.

Source: Morphing Matter Lab

Key Takeaways and Next steps.

Listening to Professor Yao was indeed exhilarating. Her insights made it clear that the concepts of morphing materials can have really profound implications for our everyday lives and for the future of our planet. I learned that sustainability isn’t just about reducing waste; it’s about rethinking design and functionality in a way that harmonizes with nature in general.

I’m deeply grateful for the real world applications of a field like GP, and I’m excited to explore how I can integrate this knowledge into projects that would benefit our world.

Once again, Thank you for these insight Professor Lining Yao. Your coming was indeed a blessing! Thank you SGI ’24 🙌

An Informal Introduction.

I’m Sergius Nyah, a pre-final year Computer Science student at University of Buea, Cameroon. ( If you’re familiar with Banff, Alberta, Canada, you should appreciate the stunning scenery of Buea as well.)
I first encountered the term “Geometry” in 9th grade (Form 4), in our Math class, and had no idea by then of its true significance.

Late 2022 was a peculiar period for me. My very special friend and past SGI fellow introduced me to the Summer Geometry Initiative. From then my immediate reaction was to research on it, connect with past fellows via LinkedIn, and bookmark it for applications, with only very little knowledge on the topic itself, apart from math theories and coding knowledge acquired in the classroom.

What the SGI means to me.

Permit me re-define what the SGI is in two ways. First from the perspective of a prospective applicant, and second as a fellow 🙂

As an applicant, the SGI is a six-week paid summer research program introducing undergraduate and graduate students to the field of geometry processing.

For current or former fellows, the SGI is an intense period of reading research papers engaged around Geometry, listening to talks you may find interesting, learning math for those without a strong math background, acquiring coding skills for students new to programming, and using this knowledge to solve problems on a daily basis, all while learning from Rock-star professors and brilliant students from around the world. Makes sense ? (Without forgetting the generous stipend 🙌🏿 and swag pack 🙂

My Experience so far!

July 8th was the much-anticipated day. That serene evening, we were officially welcomed to the Summer Geometry Initiative 2024 by Professor Justin Solomon, SGI chairman and organizer. My heart boggled with joy as I finally met him and other fellows (now friends 🙂 like Megan Grosse, Aniket Rajnish, Johan Azambou, Charuka Bandra, and a few others, with whom I had been chatting with. Proff Justin opened the floor for the tutorial week and provided us with a brief overview of what the upcoming weeks would entail.

The Tutorial week was a perfect blend of fun and fast-paced learning. Right after Prof. Justin’s welcoming, we had our first tutor for Day 1 — the “Marvelous” Professor Oded Stein, a Computer Science professor from the University of Southern California and tutorial week chair for SGI ’24. Prof. Oded introduced us to Geometry Processing (GP) and its significance to various groups, from artists to programmers. He also taught on surfaces, meshes, explaining how to represent them using triangles and faces, and how to store them using object-lists and face-lists. Additionally, we explored the different types of curvatures (normal curvature, Mean curvature, Principle curvature, Gaussian curvature, and Discrete Gaussian curvature). Next was a session on visualizing 3D data, led by Qingnan Zhou, an Engineer from Adobe Research.

On Day 2, led by Richard Liu, PhD student at the University of Chicago, we focused on parameterization and its vast potential in related fields such as computer graphics. Right after launch/exercise/siesta/rest/fun/ break 😊, we welcomed Dale Decatur, still a PhD student at the University of Chicago, who shared valuable insights on the technical know-how that would be beneficial during our research weeks.

Silvia Sellán, a pre-postdoctoral fellow at MIT and an incoming Professor at the University of Columbia, was in charge of Day 3. She spoke on the various methods of representing shapes, exploring the advantages and disadvantages of each method with regards to computer resources such as memory and processing power. The day ended with an interactive presentation from Towaki Takikawa, a PhD student at the University of Toronto, who focused on Neural Fields.

Day 4, led by Derek Liu, a research scientist at Roblox, taught on Mesh Simplification and Level of Detail (LOD). He mentioned that there are three types of Mesh simplifications: Static Simplification, which includes creating separate level of detail (LOD) models before rendering, Dynamic Simplification which provides a continuous spectrum of LOD models instead of a few discrete models, and View-Dependent Simplification where the level of detail varies within the model. Later on, Eris Zhang – a Stanford PhD student delved deeper into more technical concepts that proved to be highly beneficial for both the day’s exercises and the upcoming research weeks.

On Day 5, Dr. Nicholas Sharp, a research scientist at NVIDIA and inventor of Polyscope, a highly beneficial software tool in the GP community, led the session, marking the conclusion of the tutorial week. Dr. Nick discussed good and bad surface meshes (data), and the process of remeshing ( which involves turning a bad mesh into a good one). Additionally, we hosted a complementary session featuring guest speaker Zachary Ferguson, a postdoc researcher at MIT, who discussed handling floating points in collision detection.

In summary, Research Week 1 was led by Dr. Nicholas Sharp, research scientist at NVIDIA (A.K.A The G.O.A.T – Greatest Of All Time 🙌🏿). Our research topic focused on how “Well” various surfaces can approximate deforming meshes. I learned about chamfer distances, the Gromov-Hausdorff distance (the largest of all minimum (Chamfer) distances along two curves), and the polyline algorithm. We concluded the week with our first group article on How to Match the Wiggleness of Two Shapes, published by Artur Bogayo.

During Research Week 2, my team mates — Nicolas Pigadas and Champ – and I, led by Dr. Karthik Gopinath from Harvard Medical School explored a nouvel way of parcellating cortical meshes as 2D segments via the process of Pseudo-Rendering.

To conclude this post, I’d like to share the biggest lessons I’ve learned from the first four weeks of the SGI.

• Lesson 1: Always request a helping hand when you can’t figure things out. There’s no benefit struggling with a problem when others are just a step away. Don’t hesitate to ask for help!
• Lesson 2: Learn to adapt fast to changes. The SGI, like life in general, is fast-paced. Adapting to new research projects and working with different mentors and colleagues is a valuable skill that will significantly boost productivity.
• Lesson 3: Cultivate Self-discipline! Learning new concepts takes time. Sitting on that reading table for hours could be tiring, but please, persevere! The juice is definitely worth the squeeze!
• Lesson 4: Be transparent with your mentors/supervisors. They may be able to figure things out, but being honest about your situation demonstrates integrity and builds trust. Being honest with what went wrong is a quality people value in long-term collaborators. Don’t sugarcoat things. Tell them what went wrong. They might bite you, but won’t eat you! 😄
• Lesson 5: Do what needs doing, regardless. I started writing this blog many days ago, but only got to finish today due to a weeks-long (ongoing) power outages. And here I am now, in the dim light of a local bar at an odd hour, exposed to thieves and weird stuff (like who knows?). So do what you should do! Excuses might seem valid at the moment, but will totally seem completely irrelevant in the future.

As the SGI winds down, I’m filled with so much gratitude for this once-in-a-lifetime opportunity. I brace myself with resilience, dedication, and an insane collaboration towards the rest of our projects, with a full focus on making the most out of this tremendous initiative I’m blessed to have taken part in. A huge thank you to all my mentors, fellows-turned-friends, and everyone for making this year’s SGI what it already is and soon would be!

A luta continua!