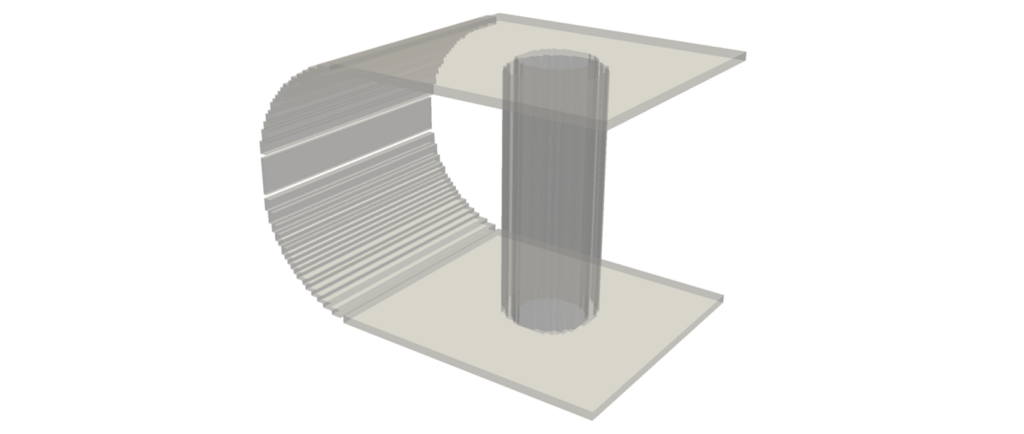

Images: (1) The Wormhole Distance Field (DF) shape. (2) The Wormhole built using DF functions, visualized using a DF/scalar field defined over a discretized space, i.e. a grid. (3) Deploying the marching cubes algorithm (https://dl.acm.org/doi/10.1145/37402.37422) to attempt to reconstruct the surface from the DF shape. (4) Resulting surface using my reconstruction algorithm based on the principles of k-nearest neighbors (kNN), for k=10. (5) Same, but from a different perspective highlighting unreconstructed areas, due to the DF shape having empty areas in the curved plane (see image 2 closely). If those areas didn’t exist in the DF shape, the reconstruction would have likely been exact with smaller k, and thus the representation would have been cleaner and more suitable for ML and GP tasks. (6) The reconstruction for k=5. (7) The reconstruction for k=5, different perspective.
Note: We could use a directional approach to knn for a cleaner reconstructed mesh, leveraging positional information. Alternatively, we could develop a connection correcting algorithm. Irrespectively to if we attempt the aforementioned optimizations or not, we can make the current implementation more optimized, as a lot less distances would need to be calculated after we organize the points of the DF shape based on their positions in the 3D space.
Intro
Well, SGI day 3 came… And it changed everything. In my mind at least. Silvia Sellán and Towaki Takikawa taught us -in the coolest and most intuitive ways- that there is so much more to shape representations. With Silvia, we discussed how one would expect to jump from one representation to another or even try to reconstruct the original shapes from representations that do not explicitely save connectivity information. With Towaki, we discussed Signed Distance Field (SDF) shapes among other stuff (shout out for building a library called haipera, that will definetely be useful to me) and the crazy community building crazy shapes using them. All the newfound knowledge got me thinking. Again.
Towaki was asked if there are easier/automated ways to calculate the necessary SDF functions because it would be insane to build -for e.g.- SDF cars by hand. His response? These people are actually insane! And I wanted to get a glimpse of that insanity, to figure out how to build the wormhole using Distance Field (DF) functions. Of course, my target final shape is a lot easier and it turned out that the implementation was far easier than calculating vertices and faces manually (see Wormhole I)! Then, Silvia’s words came to mind: each representation is suitable for different tasks, i.e., a task that is trivial for DF representations might be next to impossible for other representasions. So, creating a DF car is insane, but using functions to calculate the coordinates of a mesh grid car would be even more insane! Fun fact from Silvia’s slides: “The first real object ever 3D scanned and rendered was a WV Beetle by the legendary graphics researcher Ivan Sutherland’s lab (and the car belonged to his wife!)” and it was done manually:

Image (8): Calculating the coordinates of vertices and the faces to design the mesh of a Beetle manually! Geometric Processing gurus’ old school hobbies.
Method
Back to the DF Wormhole. The high-level algorithm for the DF Wormhole is attached below (for the implementation, visit this GitHub repo:

Having my DF Wormhole, the problem of surface reconstruction arose. Thankfully, Silvia had already made sure we got, not only an intuitive understanding of multiple shape representations in 2D and 3D, but also how to jump from one to another and how to reconstruct surfaces from discretized representations. It intrigued me what would happen if I used the marching cubes algorithm on my DF shape. The result was somewhat disappointing (see image 3).
Yet, I couldn’t just let it go. I had to figure out something better. I followed the first idea that came to mind: k-Neirest Neighbors (kNN). My hypothesis was that although the DF shape is in 3D, it doesn’t have any volumetric data. The hypothetical final shape is comprised by surfaces so kNN makes sense; the goal is to find the nearest neighbors and create a mechanism to connect them. It worked (see images 4, 5, 6, 7)! A problem became immediately apparent: the surface was not smooth in certain areas, but rather blocky. Thus, I developed an iterative smoothing mechanism that repositions the nodes based on the average of the coordinates of their neighbors. At 5 iterations the result was satisfying (see image 8). Below I attach the algorithm, (for the implementation, visit this GitHub repo: https://github.com/NIcolasp14/MIT_SGI-Wormhole). Case closed.

Q&A
Q: Why did I call my functions Distance Field functions (DFs) and not Signed Distance Field functions (SDFs)?
A: Because the SDF representation requires some points to have a negative value in relation to a shape’s surface (i.e., we have a negative sign for points inside the shape). In the case of the hollow shapes, such as the hollow cube and cylinder, we replace the negative signs of the inner parts of the outer shapes with positive signs, via the statement max(outer_shape, -inner_shape). Thus, our surfaces/hollow shapes only have 0 values on the surface and positive elsewhere. These type of distance fields are called unsigned (UDFs).
Q: What about the semi-cylinder?
A: The final shape of the semi-cylinder was defined to have negative values inside the radius of the semi-cylinder, 0 on the surface and positive elsewhere. But in order to remove the caps, rather than subtracting an inner cylinder, I gave them a positive value (e.g. infinity). This contradicts the definition of SDFs and UDFs, which measure distance in a continuous way. So, the semi-cylinder would be referred to as a discontinuous distance function (or continuous with specific discontinuities by design).
Future considerations
Using the smoothing mechanism and not using it has a trade off. The smooting mechanism seems to remove more faces -that we do want to have in our mesh-, than if we do not use it (see images 9, 10). The quality of the final surface certaintly depends on the initial DF shape (which indeed had empty spaces, see image 2 closely) and the hyperparameter k of kNN. Someone would need to find the right balance between the aforementioned parameters and the smoothing mechanism or even reconsider how to create the initial Wormhole DF shape or/and how to reposition the vertices, in order to smooth the surfaces more effectively. Finally, all the procedures of the algorithm can be optimized to make the code faster and more efficient. Even the kNN algorithm can be optimized: not every pair must be calculated to compare distances, because we have positional information and thus we can avoid most of the kNN calculations.

Images: (9) Mesh grid using only the mechanism that connects the k-nearest neighbors for k=5, (10) Mesh grid after the additional use of the smoothing mechanism.
Wormhole: The end