Last week, we looked into Voronoi tessellations and their potential for high dimensional sampling and integral approximations.
When we have a very complicated high-dimensional function, it can be very challenging to compute its integral in a given domain. A standard way to approximate it is through Monte Carlo integration
Monte Carlo integration
Monte Carlo integration is a technique consisting of querying the integrand function f at N random locations uniformly, taking the average, and then multiplying the region’s volume:
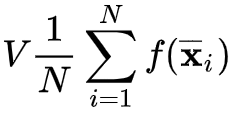
The law of large numbers ensures that, in the limit, this quantity approximates the actual integral better and better.
Okay, but the points are sampled i.i.d. uniformly, which might not be optimal to compute the integral’s value from a very small sample size. Maybe we can find a way to guide the sampling and leverage prior knowledge we might have about the sample space.
Okay, and maybe the points are not extracted i.i.d. What if we have no control over the function – maybe it’s some very big machine in a distant factory, or an event occurring once in a decade. If we can’t ensure that the points are i.i.d. we just can’t use Monte Carlo integration.
Therefore, we will investigate whether we can use Voronoi tessellations to overcome this limitation.
Voronoi Tessellation
A Voronoi tessellation is a partition of the space according to the following rules:
- We start with some “pivot” points pi in the space (which could be the points at which we evaluate the integrand function)

- Now, we create as many regions as there are initial pivot points defined as follows: a point x in the space belongs to the region of the point pi if the point pi is the closest pivotal point to x :

Voronoi tessellation is essentially one iteration of k-means clustering where the centroids are the pivotal points pi and the data to cluster are all the points x in the domain
Some immediate ideas here:
- We can immediately try out “Voronoi integration”, where we multiply the value of the integrand at each starting point f(pi) by the volume of its corresponding region, summing them all up, and see how it behaves compared to Monte Carlo integration (especially in high dimensions)
- We can exploit Bayesian optimisation to guide the sampling of the points pi as we don’t require them to be i.i.d. unlike Monte Carlo integration
- We can exploit prior knowledge on the integration domain to weight the areas by a measure
In the next blog posts, we will see some of these ideas in action!