SGI Fellows: Melisa Oshaini Arukgoda, David Uzor, Lydia Madamopouloua, Joana Owusu-Appiah
Mentors: Oliver Gross, Quentin Becker
SGI Volunteer: Denisse Garnica

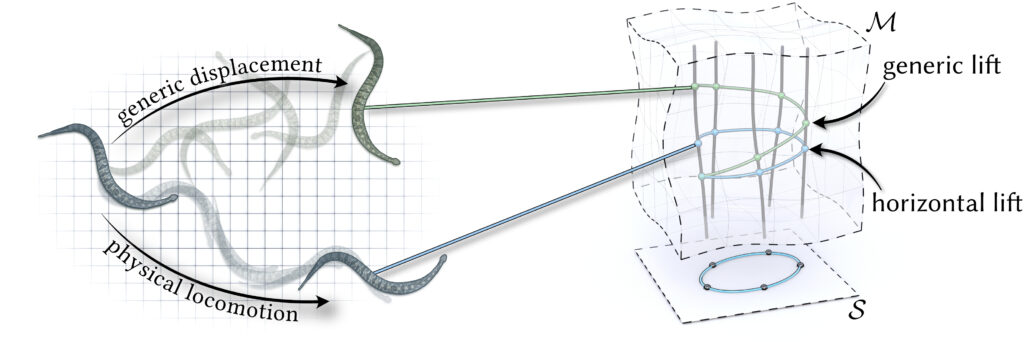
In Week 4 of SGI, we worked on a simulation project that built on the previous work of our Mentors Oliver Gross and Quentin Becker: motion from shape change and inverse geometric locomotion – to put it simply, identifying the sequence of shapes (gait) that a body will need to morph into in order to follow a specific path, without the influence of external forces. In nature, we see this behaviour in many different organisms: Stingrays, snails, Cats (when adjusting their position to allow them to land on their feet after falling), and snakes. Unlike standard physics-based simulations that rely on heavy Newtonian calculations of forces and accelerations, the approach we worked with reformulated the problem as an optimization over shape changes alone. By leveraging conservation laws through geometric mechanics, we could avoid full force-based simulations and instead compute efficient gaits directly — a shift that makes the process both faster and more generalizable.
Motion from Shape Change
Snake-like robots are fascinating because they don’t rely on wheels or legs for movement. Instead, they move by changing their shape over time. This type of motion is called geometric locomotion. By coordinating joint angles in a specific sequence, the robot can “slither” forward, turn, or even back up. Mathematically, we describe this by mapping changes in shape (joint angles) to displacements in space. The beauty of this approach is that the same principles apply whether the robot is operating on flat ground or navigating through more complex environments.
To simulate this, we used Python code that defines the joint angles, applies forward integration, and produces the resulting trajectory. By running sequences of positive and negative angles, we could generate gaits (movement patterns) and measure their effectiveness. Parameters like amplitude, phase shift, and anisotropy ratio all influence how efficient or smooth the motion becomes.
Inverse Geometric Locomotion
While forward motion planning tells us what happens when we execute a gait, inverse geometric locomotion helps us answer the opposite question: what shape sequence do we need to reach a target position or avoid an obstacle? This is formulated as an optimization problem. We define objectives such as “reach this point,” “avoid that obstacle,” or “turn left”, and then optimize the gait until the resulting motion matches the objective.
Here, the gradient descent optimization algorithm is applied to adjust the sequence of joint angles. Our experiments demonstrated that even when constraints are applied (such as broken joints or limited power), the robot can often still achieve meaningful locomotion by adapting its gait.
Breaking and Fixing Robots
One of the challenges with snake robots is robustness. What happens if a joint breaks? We simulated this by disabling certain joints and observing the effect. Unsurprisingly, the robot’s gait efficiency drops, but not all joints are equally important. Some failures severely reduce mobility, while others can be compensated for.
To “fix” the robot, we rerun the optimization process under the new constraints. By adapting the gait, the robot can still move, albeit with reduced performance. This kind of resilience is critical for real-world applications, where hardware failures are inevitable.
Avoiding Obstacles
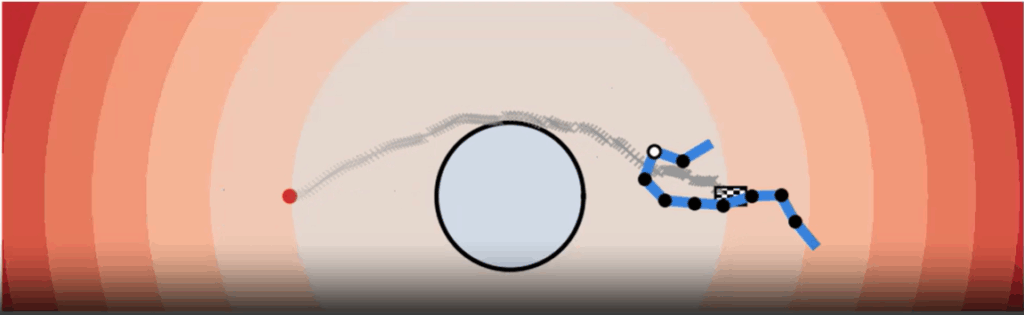
Another core part of our experiments was obstacle avoidance. Instead of using explicit geometry, we represented obstacles as implicit functions (mathematical descriptions where the function is positive outside, negative inside, and zero at the boundary). This allows smooth and flexible definitions of obstacles of any shape.
The robot’s motion planner then ensures that the trajectory stays in the safe (positive) region. We tested this with different obstacle shapes and verified that the snake robot can successfully reconfigure its gait to slither around barriers.
Applications
This computational framework for inverse geometric locomotion opens doors for several interesting applications, particularly in the fields of animation and robotics. The video below shows the snake robot in action (courtesy of the MiniRo Lab at the University of Notre Dame), loaded with the shape sequences from the simulation.