Our work was carried out under the mentorship of Yi Zhuo from Adobe Research, whose guidance was instrumental and very much appreciated. We also thank Sanghyun Son , the first author of the original DMesh and DMesh++ , for generously sharing his insights and providing invaluable input.
Article Composed By :
Gabriel Isaac Alonso Serrato
in collaboration with
Amruth Srivathsan
Click Below to Try :
INTRODUCTION
This article introduces Differentiable Mesh++ (DMesh++), exploring what a mesh is, why discrete mesh connectivity blocks gradient flow, how probabilistic faces restore differentiability, and how a local, GPU-friendly tessellation rule replaces a global weighted Delaunay step. We close with a practical optimization workflow and representative applications.
WHAT IS A MESH?
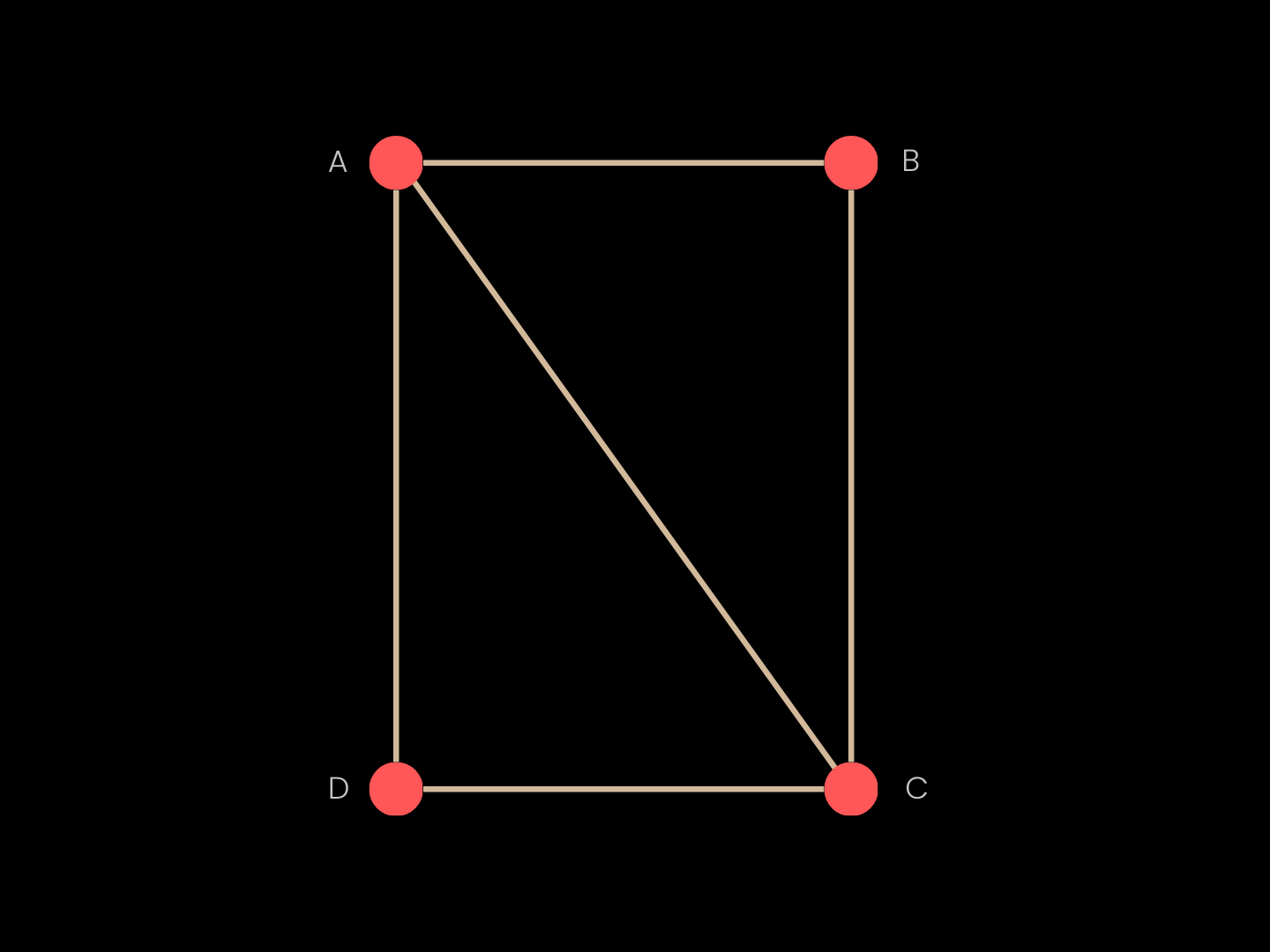
A triangle mesh combines geometry and topology. Geometry is given by vertex coordinates (named points in space such as A, B, C, and D) while topology specifies which vertices are connected by edges and which triplets form triangular faces (e.g., ABC, ACD). Together, these define shape and structure in a compact representation suitable for rendering and computation on complex surfaces.
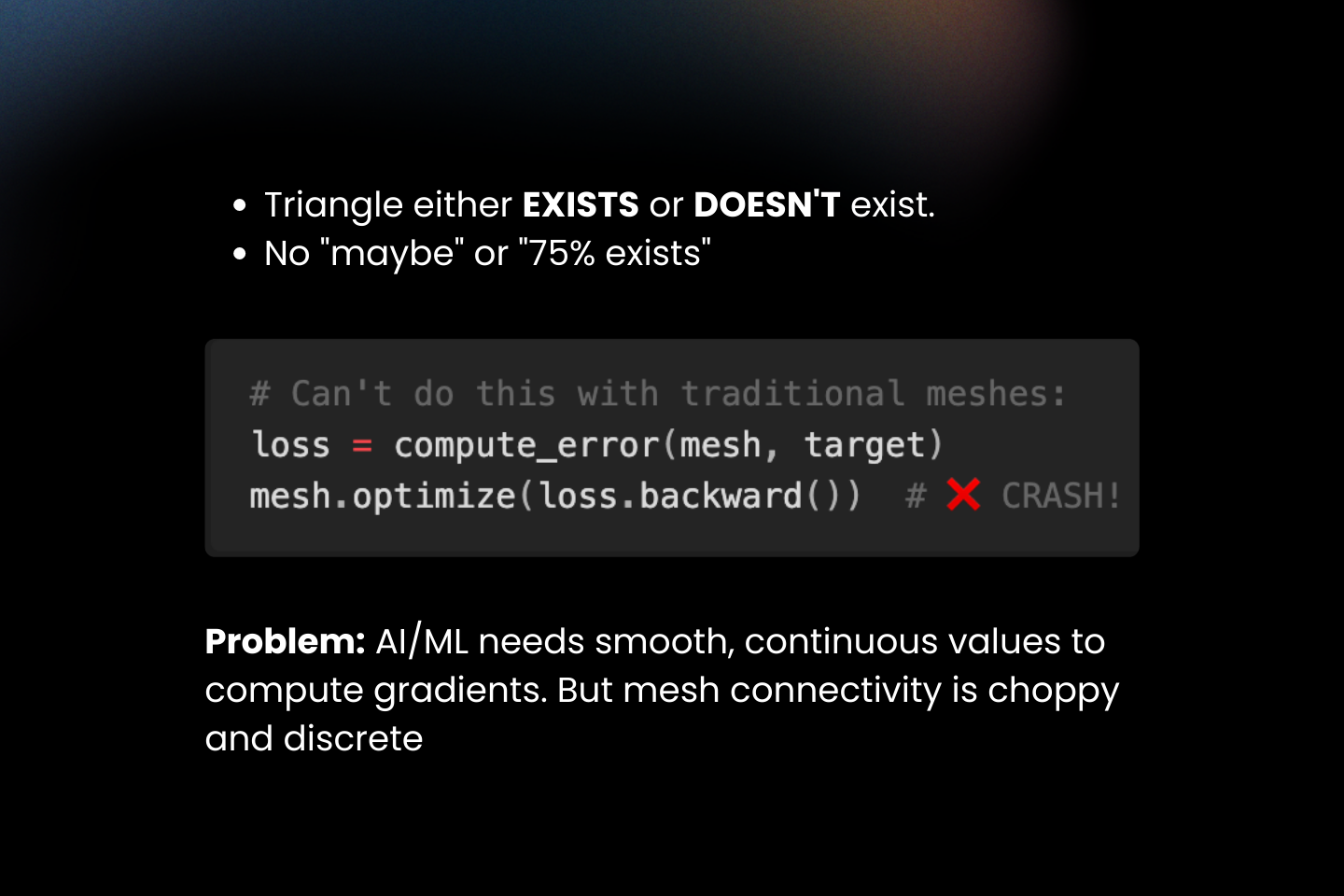
Why Traditional Meshes Fight Gradients?
Classical connectivity is discrete: a triangle either exists or it does not. Gradient-based learning, however, requires smooth changes. When connectivity flips on or off, derivatives vanish or become undefined through those choices, preventing gradients from flowing across topology changes and limiting end-to-end optimization
Differentiable Meshes
Gradients are essential for learning-based pipelines, where losses may be defined in image space, perceptual space, or 3D metric space.
Differentiable formulations make it possible to propagate error signals from rendered observations or physical constraints back to vertex positions, enabling tasks such as inverse rendering, shape optimization, and end-to-end 3D reconstruction. This bridges the conceptual gap between discrete geometry and continuous optimization, allowing mesh-based representations to function as both modeling primitives and trainable structures.
How DMesh++ Works
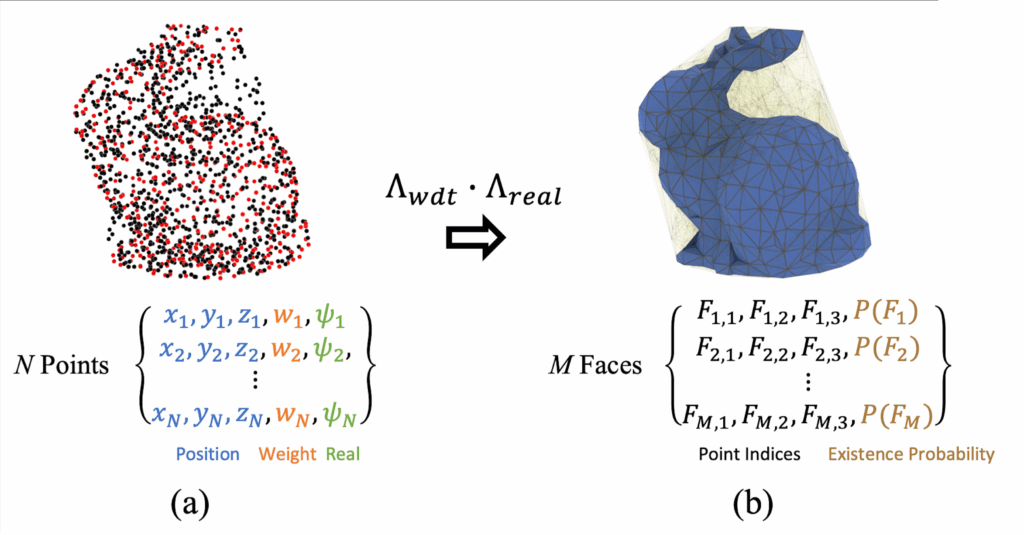
DMesh++ makes meshing a differentiable, GPU-native step. Each point carries learnable features (position, a “realness” score ψ, and optional channels).
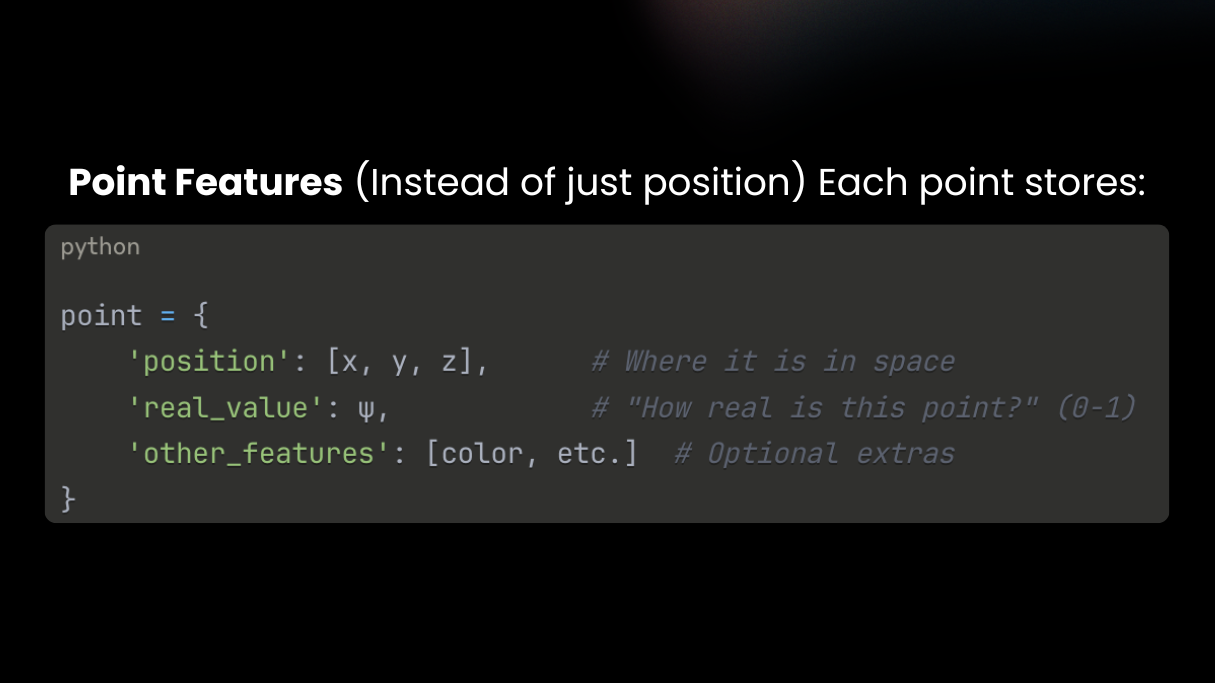
A soft tessellation function turns any triplet into a triangle weight rather than a hard on/off face.
During training, losses back-propagate to both positions and features, so connectivity can evolve smoothly.
The “One-Line” Idea in DMesh++
In DMesh++, we replace WDT ( Λwdt )
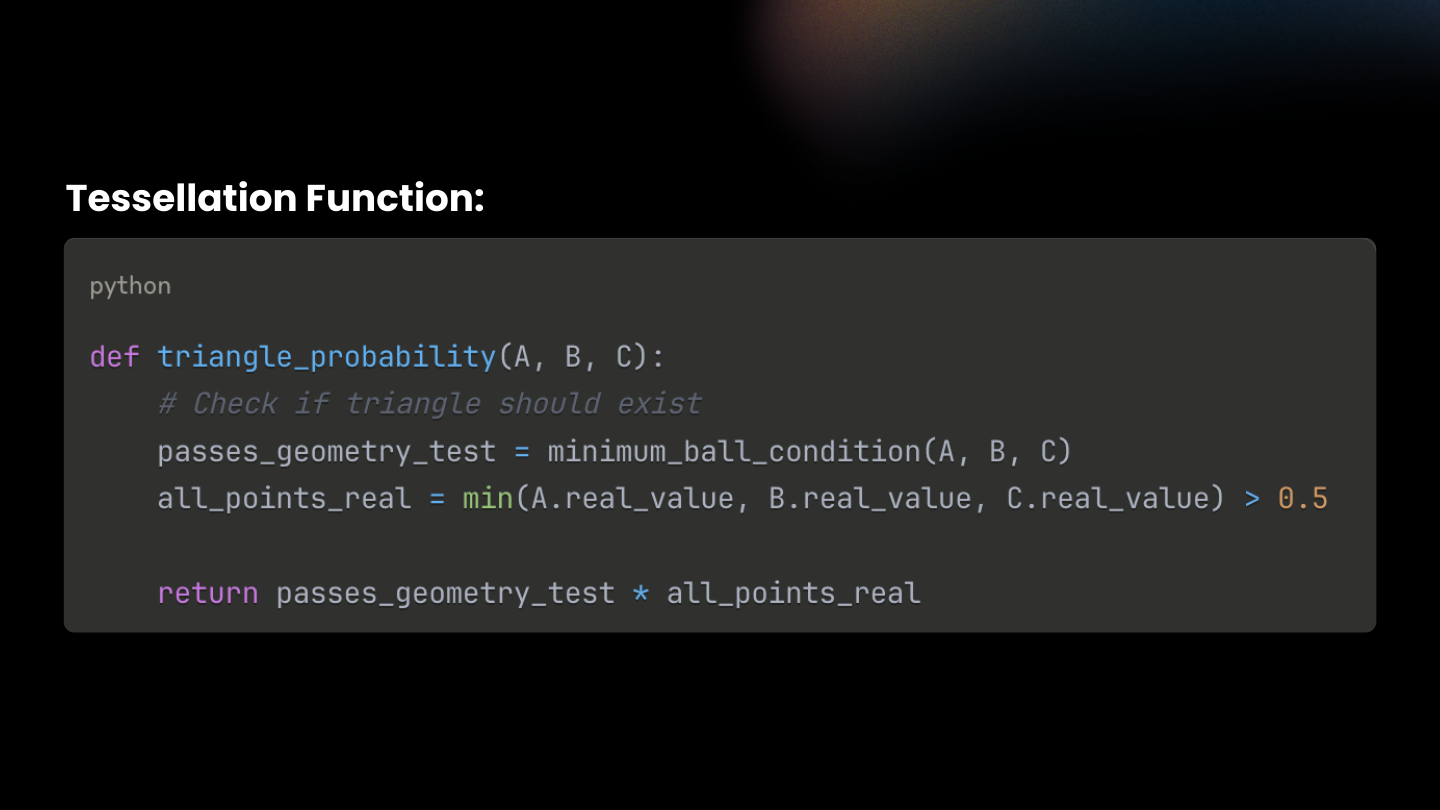
with a local Minimum-Ball test ( Λmin ) when scoring each candidate face. Instead of rebuilding a global structure, we only check the smallest ball touching the face’s vertices and see if any other point lies inside it. This can be done quickly with k-nearest neighbor search on the GPU. The face probability is now:
Λ(F) = Λmin(F) × Λreal(F)
- Λmin(F) says, “Is this face even eligible as part of a good tessellation?” (now via the Minimum-Ball test)
- Λreal(F) says, “Is this face on the real surface?” (a differentiable min over the per-point realness ψ)
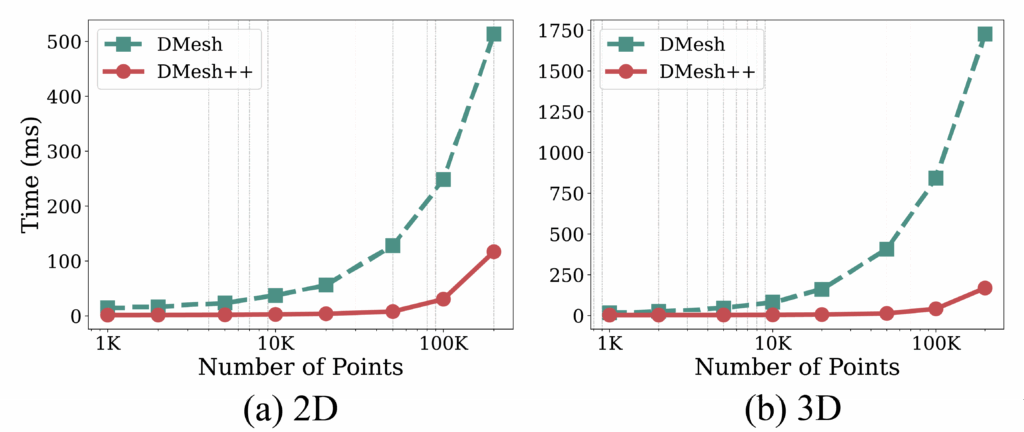
This swap reduces the effective evaluation cost from O(N) (WDT) to O(log N) with k-NN and parallelization, in practice, achieving speeds up to 16× faster in 2D and 32× faster in 3D, with significant memory savings.
Minimum-Ball, Explained
Pick a candidate face F (segment in 2D, triangle in 3D). Compute its minimum bounding ball BF : the smallest ball that touches all vertices of F.
Now check: is any other point strictly inside that ball? If no, F passes. If yes, reject. That’s the Minimum-Ball condition. (It’s a subset of Delaunay, so you inherit good triangle quality and avoid self-intersections.)
DMesh++ makes this soft and differentiable. It computes a signed distance between BF and the nearest other Point and runs it through a sigmoid to get Λmin :
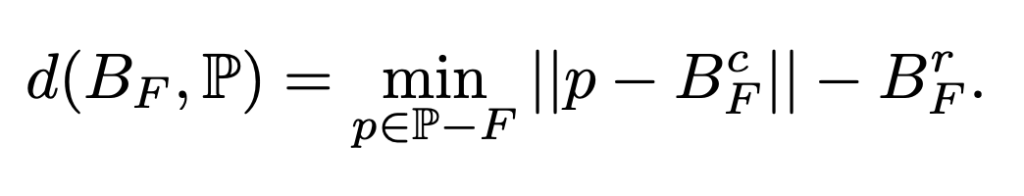
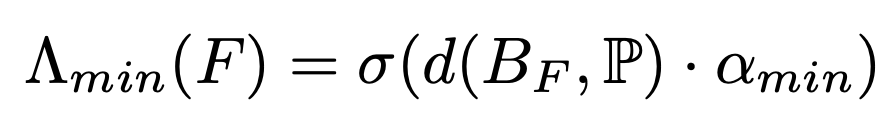
Minimum-Ball Playground:
Click here to try:
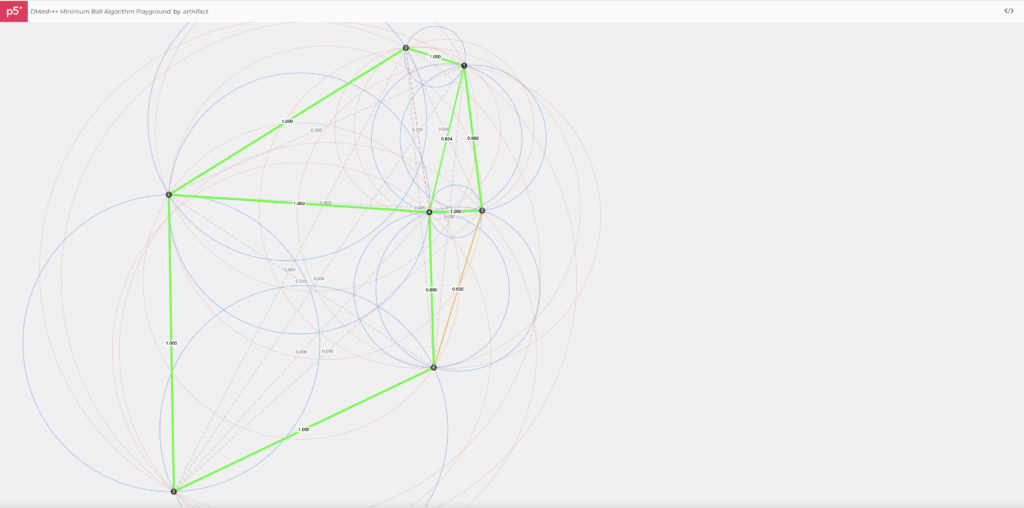
How to use it?
Click on the canvas to drop points. Every pair of points becomes a candidate edge F. We draw the minimum ball BF (the smallest circle touching the two endpoints) and compute a soft eligibility via a sigmoid of its clearance to the nearest third point:
Because faces are probabilistic, the topology can change cleanly during optimization. You don’t hand-edit connectivity; it emerges from the features.
Recap: A Practical Optimization Workflow
Start: Begin with points (positions + realness ψ)
Candidates: Form nearby faces (via k-NN)
Minimum-Ball: For each face, find the smallest ball touching its vertices (if no point is inside, it’s valid) → gives Λₘᵢₙ
Weight by Realness: Multiply by vertex ψ to get final probability Λ = Λₘᵢₙ × Λᵣₑₐₗ
Optimize: Compute the loss (e.g., Chamfer), and backpropagate to update the points and ψ
Output: Keep high-Λ faces → final differentiable mesh
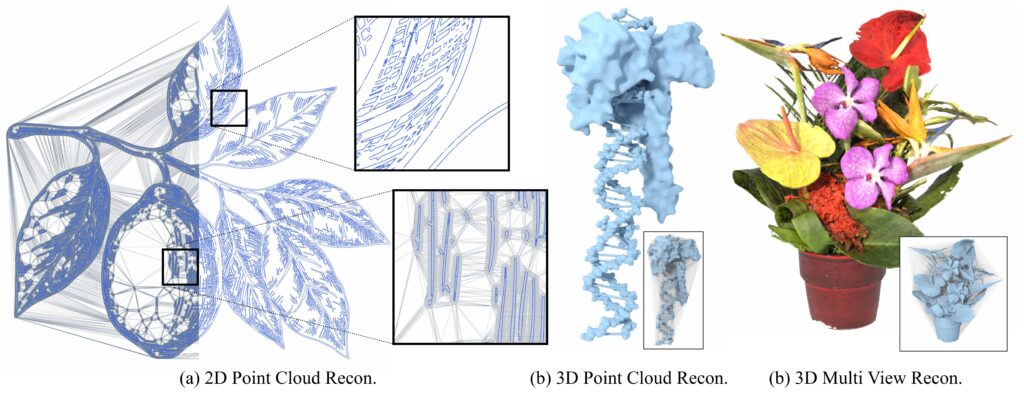
Some Applications of DMesh++
DMesh++ demonstrates how differentiable meshes can power real applications. Here are some ideas:
Generative Design: Train models that evolve shapes and topology for creative or engineering tasks without manual remeshing.
Adaptive Level of Detail: Automatically refine or simplify geometry based on learning signals or rendering needs.
Feature-Aware Reconstruction: Learn geometric structure, merge fragments, or fill missing regions directly through optimization.
Neural Simulation: Enable physics or visual simulations where mesh shape and motion are optimized end-to-end with gradients.
Future Directions
Looking ahead, future work on DMesh++ could focus on improving usability and scalability, for example, by developing more accessible APIs, real-time visualization tools, and integration with common 3D software. On the algorithmic side, enhancing the tessellation functions for higher precision and stability, expanding support for non-manifold and hybrid volumetric surfaces, and further optimizing GPU kernels for large-scale datasets could make differentiable meshing faster, more robust, and easier to adopt across geometry processing, simulation, and machine learning workflows.