Author: ualibek

Categories
Research

A Brief Tour of Discrete Morse Theory

One will probably ask “what is even discrete morse theory?”
A good question. But a better question is, “what is even morse theory?”

A Detour to Morse Theory

It would be a sin to not include this picture of a torus on any text for an introduction to Morse Theory.

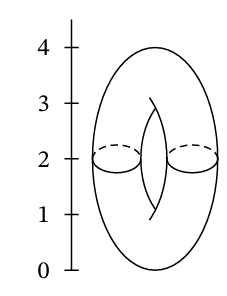
Consider a height function \(f\) defined on this torus \(T\). Let \(M_z = \{x\in T | f(x)\le z\}\), i.e., a slice of the torus below level \(z\).

Morse theory says critical points of \(f\) can tell us something about the topology of the shape. The critical points can be determined by recalling from calculus that those points correspond to the points where the partial derivatives all equal zero. Then, the four critical points on the torus at heights 0, 1, 3, and 4 can be identified, each of which correspond to topological changes in the sublevel sets (\(M_z\)) of the function. In particular, imagine a sequence of sublevel sets \(M_z\) with ever increasing \(z\) values. Notice that each time we pass through a critical point, there is an important topological change in the sublevel sets.

  • At height 0, everything starts with a point
  • At height 1, a 1-handle is attached
  • At height 3, another 1-handle is added
  • Finally, at height 4, the maximum is reached, and a 2-handle is attached, capping off the top and completing the torus.

Through this process, Morse theory illustrates how the torus is constructed by successively attaching handles, with each critical point indicating a significant topological step.

Discretizing Morse Theory

Originally, Forman introduces discrete Morse Theory to let it inherit many similarities from its smooth counterpart, but it deals with discretized objects like CW complexes or a simplicial complex. In particular, we will focus on discrete morse theory on a simplicial complex.

Definition. Let \(K\) be a simplicial complex. A discrete vector field V on \(K\) is a set of pairs of cells \((\sigma, \tau) \in K\times K\), with \(\sigma\) a face of \(\tau\), such that each cell of \(K\) is contained in at most one pair of \(V\).
Definition. A cell \(\sigma\in K\) is critical with respect to \(V\) if \(\sigma\) is not contained in any pair of \(V\).

A discrete vector filed V can be readily visualized as a set of arrows like below.

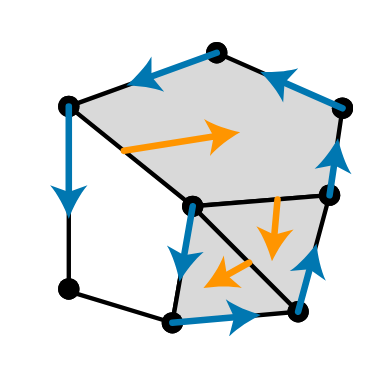
Figure 1. The bottom left vertex is critical

Definition. Let \(V\) be a discrete vector field. A \(V\)-path \(\Gamma\) from a cell \(\sigma_0\) to a cell \(\sigma_r\) is a sequence \((\sigma_0, \tau_0, \sigma_1, \dots, \tau_{r-1}, \sigma_r)\) of cells such that for every \(0\le i\le r-1:\)
$$
\sigma_i \text{ is a face of } \tau_i \text{ with } (\sigma_i, \tau_i \in V) \text{ and } \sigma_{i+1} \text{ is a face of } \tau_i \text{ with } (\sigma_{i+1}, \tau_i)\notin V.
$$\(\Gamma\) is closed if \(\sigma_0=\sigma_r\), and nontrivial if \(r>0\).

Definition. A discrete vector field V is a discrete gradient vector field if it contains no nontrivial closed V-paths.

Finally, with this in mind, we can define what properties should a Morse function satisfy on a given simplicial complex \(K\).

Definition. A function \(f: K\rightarrow \mathbb{R}\) on the cells of a complex K is a discrete Morse function if there is a gradient vector field \(V_f\) such that whenever \(\sigma\) is a face of \(\tau\) then
$$
(\sigma, \tau)\notin V_f \text{ implies } f(\sigma) < f(\tau) \text{ and } (\sigma, \tau)\in V_f \text{ implies } f(\sigma)\ge f(\tau).
$$\(V_f\) is called the gradient vector field of \(f\).

Definition. Let \(V\) be a discrete gradient vector field and consider
the relation \(\leftarrow_V\) defined on \(K\) such that whenever \(\sigma\) is a face of \(\tau\) then
$$
(\sigma, \tau)\notin V \text{ implies } \sigma\leftarrow_V \tau \text { and } (\sigma, \tau)\in V \text{ implies } \sigma\rightarrow_V \tau.
$$
Let \(\prec_V\) be the transitive closure of \(\leftarrow_V\) . Then \(\prec_V\) is called the partial order induced by V.

We are now ready to introduce one of the main theorems of discrete Morse Theory.

Theorem. Let \(V\) be a gradient vector field on \(K\) and let \(\prec\) be a linear extension of \(\prec_{V}\). If \(\rho\) and \(\psi\) are two simplices such that \(\rho \prec \psi\) and there is no critical cell \(\phi\) with respect to \(V\) such that \(\rho\prec\phi\preceq\psi\), then \(\kappa(\psi)\) collapses (homotopy equivalent) to \(\kappa(\rho)\).
Here, $$\kappa(\sigma) = closure(\cup_{\rho\in K; \rho\preceq\sigma}\rho)$$ an equivalent of sublevel set in the discrete setting.

This theorem says that given a gradient vector filed to a simplicial complex, and we consider how it is built over time by bringing each simplex in \(\prec\)’s order, then the topological changes happen only at the critical points determined by the gradient vector field. This strikingly is reminiscent of the case with the torus above.

This perspective is not only conceptually elegant but also computationally powerful: by identifying and retaining only the critical simplices, we can drastically reduce the size of our complex while preserving its topology. In fact, several groups of researchers have already utilized the discrete morse theory to simplify a function by removing topological noise.

Reference

  • Bauer, U., Lange, C., & Wardetzky, M. (2012). Optimal topological simplification of discrete functions on surfaces. Discrete & computational geometry, 47(2), 347-377.
  • Forman, R. (1998). Morse theory for cell complexes. Advances in mathematics, 134(1), 90-145.
  • Scoville, N. A. (2019). Discrete Morse Theory. United States: American Mathematical Society.
Categories
Research

Topology Control: Training a DeepSDF (1/2)

SGI Fellows:
Stephanie Atherton, Marina Levay, Ualibyek Nurgulan, Shree Singhi, Erendiro Pedro

In the Topology Control project mentored by Professor Paul Kry and project assistants Daria Nogina and Yuanyuan Tao, we sought to explore preserving topological invariants of meshes within the framework of DeepSDFs. Deep Signed Distance Functions are a neural implicit representation used for shapes in geometry processing, but they don’t come with the promise of respecting topology. After finishing our ML pipeline, we explored various topology-preserving techniques through our simple, initial case of deforming a “donut” (torus) into a mug.

DeepSDFs

Signed Distance Field (SDF) representation of a 3D bunny. The network predicts the signed distance from each spatial point to the surface. Source: (Park et al., 2019).

Signed Distance Functions (SDFs) return the shortest distance from any point in 3D space to the surface of an object. Their sign indicates spatial relation: negative if the point lies inside, positive if outside. The surface itself is defined implicitly as the zero-level set: the locus where \(\text{SDF}(x) = 0 \).

In 2019, Park et al. introduced DeepSDF, the first method to learn a continuous SDF directly using a deep neural network (Park et al., 2019). Given a shape-specific latent code \( z \in \mathbb{R}^d \) and a 3D point \( x \in \mathbb{R}^3 \), the network learns a continuous mapping:

$$
f_\theta(z_i, x) \approx \text{SDF}^i(x),
$$

where \( f_\theta \) takes a latent code \( z_i \) and a 3D query point \( x \) and returns an approximate signed distance.

The training set is defined as:

$$
X := {(x, s) : \text{SDF}(x) = s}.
$$

Training minimizes the clamped L1 loss between predicted and true distances:

$$
\mathcal{L}\bigl(f_\theta(x), s\bigr)
= \bigl|\text{clamp}\bigl(f_\theta(x), \delta\bigr) – \text{clamp}(s, \delta)\bigr|
$$

with the clamping function:

$$
\text{clamp}(x, \delta) = \min\bigl(\delta, \max(-\delta, x)\bigr).
$$

Clamping focuses the loss near the surface, where accuracy matters most. The parameter \( \delta \) sets the active range.

This is trained on a dataset of 3D point samples and corresponding signed distances. Each shape in the training set is assigned a unique latent vector \( z_i \), allowing the model to generalize across multiple shapes.

Once trained, the network defines an implicit surface through its decision boundary, precisely where \( f_\theta(z, x) = 0 \). This continuous representation allows smooth shape interpolation, high-resolution reconstruction, and editing directly in latent space.

Training Field Notes

We sampled training data from two meshes, torus.obj and mug.obj using a mix of blue-noise points near the surface and uniform samples within a unit cube. All shapes were volume-normalized to ensure consistent interpolation.

DeepSDF is designed to intentionally overfit. Validation is typically skipped. Effective training depends on a few factors: point sample density, network size, shape complexity, and sufficient epochs.

After training, the implicit surface can be extracted using Marching Cubes or Marching Tetrahedra to obtain a polygonal mesh from the zero-level set.

Training Parameters
SDF Delta1.0
Latent Mean0.0
Latent SD0.01
Loss FunctionClamped L1
OptimizerAdam
Network Learning Rate0.001
Latent Learning Rate0.01
Batch Size2
Epochs5000
Max Points per Shape3000
Network Architecture
Latent Dimension16
Hidden Layer Size124
Number of Layers8
Input Coordinate Dim3
Dropout0.0
Point Cloud Sampling
Radius0.02
Sigma0.02
Mu0.0
Number of Gaussians10
Uniform Samples5000

For higher shape complexity, increasing the latent dimension or training duration improves reconstruction fidelity.

Latent Space Interpolation

One compelling application is interpolation in latent space. By linearly blending between two shape codes \( z_a \) and \( z_b \), we generate new shapes along the path

$$
z(t) = (1 – t) \cdot z_a + t \cdot z_b,\quad t \in [0,1].
$$

Latent space interpolation between mug and torus.

While DeepSDF enables smooth morphing between shapes, it exposes a core limitation: a lack of topological consistency. Even when the source and target shapes share the same number of genus, interpolated shapes can exhibit unintended holes, handles, or disconnected components. These are not artifacts, they reveal that the model has no built-in notion of topology.

However, this limitation also opens the door for deeper exploration. If neural fields like DeepSDF lack an inherent understanding of topology, how can we guide them toward preserving it? In the next post, we explore a fundamental topological property—genus—and how maintaining it during shape transitions could lead us toward more structurally meaningful interpolations.

References