SGI Fellows:
Stephanie Atherton, Marina Levay, Ualibyek Nurgulan, Shree Singhi, Erendiro Pedro
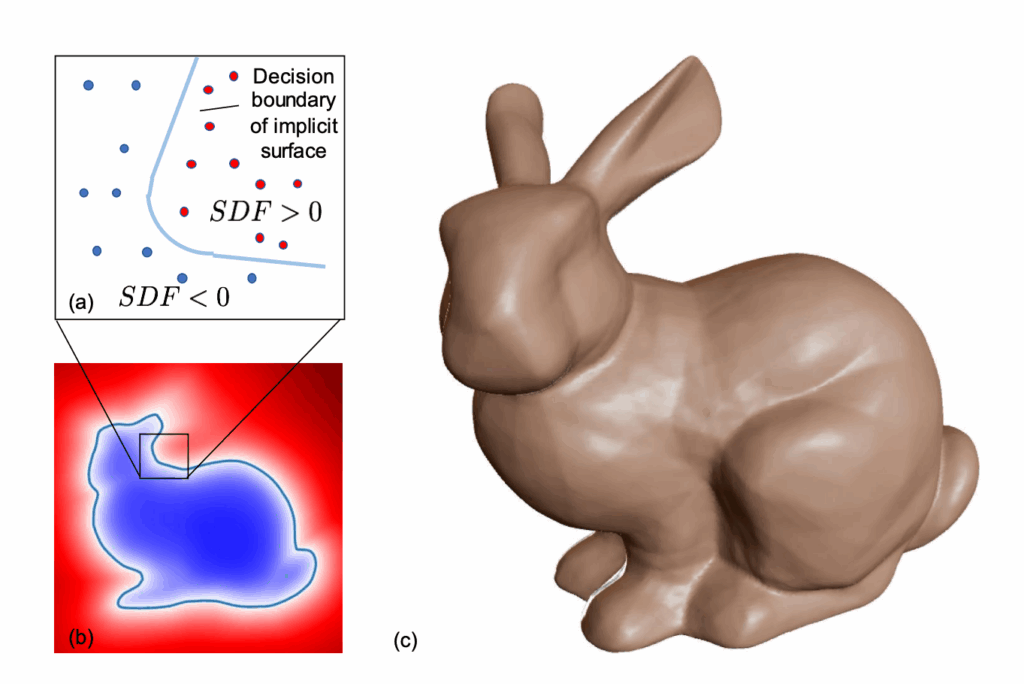
Recall (from post 1/2) that while DeepSDFs are a powerful shape representation, they are not inherently topology-preserving. By “preserving topology,” we mean maintaining a specific topological invariant throughout shape deformation. In low-dimensional latent spaces \(z_{\text{dim}} = 2\), linear interpolation between two topologically similar shapes can easily stray into regions with a different genus, breaking that invariant.
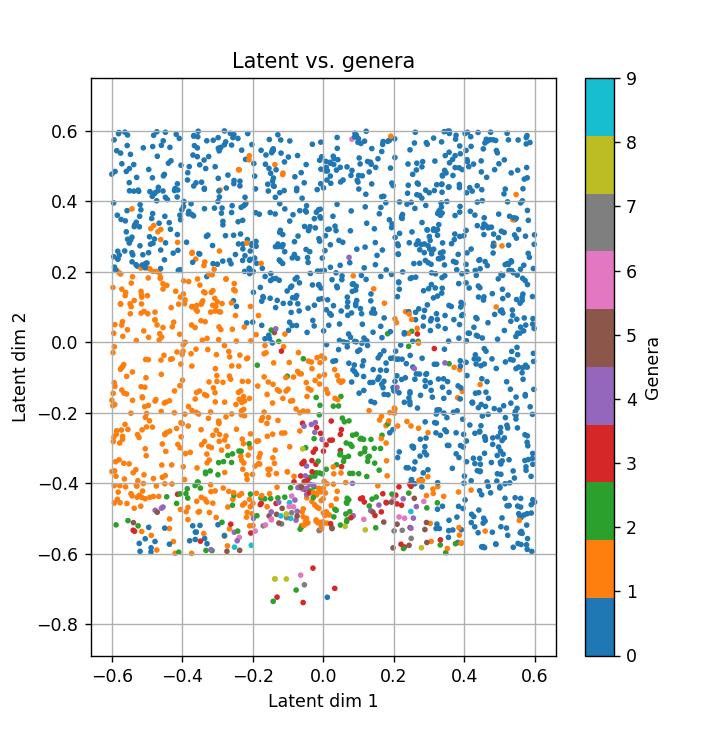
Higher-dimensional latent spaces may offer more flexibility—potentially containing topology-preserving paths—but these are rarely straight lines. This points to a broader goal: designing interpolation strategies that remain within the manifold of valid shapes. Instead of naive linear paths, we focus on discovering homotopic trajectories—routes that stay on the learned shape manifold while preserving both geometry and topology. In this view, interpolation becomes a trajectory-planning problem: navigating from one latent point to another without crossing into regions of invalid or unstable topology.
Pathfinding in Latent Space
Suppose you are a hiker hoping to a reach a point \(A\) from a point \(B\) amidst a chaotic mountain range. Now your goal is to plan your journey so that there will be minimal height change in your trajectory, i.e., you are a hiker that hates going up and down much! Fortunately, an oracle gives us a magical device, let us call it \(f\), that can give us the exact height of any point we choose. In other words, we can query \(f(x)\) for any position \(x\), and this device is differentiable, \(f'(x)\) exists!
Metaphors aside, the problem of planning a path from a particular latent vector \(A\) to another \(B\) in the learned latent space would greatly benefit from another auxiliary network that learns the mapping from the latent vectors to the desired topological or geometric features. We will introduce a few ways to use this magical device – a simple neural network.
Gradient as the Compass
Now the best case scenario would be to stay at the same height for the whole of the journey, no? This greedy approach puts a hard constraint on the problem, but it also greatly reduces the possible space of paths to take. For our case, we would love to move toward the direction that does not change our height, and this set of directions precisely forms the nullspace of the gradient.
No height change in mathematical terms means that we look for directions where the derivatives equal zero, as in
$$D_vf(x) = \nabla f(x)\cdot v = 0,$$
where the first equality is a fact of the calculus and the second shows that any desirable direction \(v\in \text{null}(\nabla f(x))\).
This does not give any definitive directions for a position \(x\) but a set of possible good directions. Then a greedy approach is to take the direction that aligns most with our relative position against the goal – the point \(B\).
Almost done, but the problem is that if we always take steps with the assumption that we are on the correct isopath, we would end up accumulating errors. So, we actually want to nudge ourselves a tiny bit along the gradient to land back on the isopath. Toward this, let \(x\) be the current position and \(\Delta x=\alpha \nabla f(x) + n\), where \(n\) is the projection of \(B-x\) to \(\text{null}(\nabla f(x))\). Then we want \(f(x+\Delta x) = f(B)\). Approximate
$$f(B) = f(x+\Delta x) \approx f(x) + \nabla f(x)\cdot \Delta x,$$
and substituting for \(\Delta x\), see that
$$f(x) + \nabla f(x) \cdot (\alpha\nabla f(x) + n) \
\Longleftrightarrow
\alpha \approx \frac{f(B) – f(x)}{|\nabla f(x)|^2}.$$
Now we just take \(\Delta x = \frac{f(B) – f(x)}{|\nabla f(x)|^2}\nabla f(x) + \text{proj}_{\text{null}(\nabla f(x))} (B- x)\) for each position \(x\) on the path.
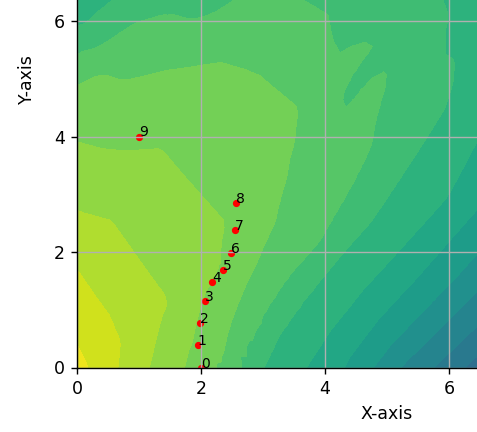
Optimizing Vertical Laziness
Sometimes it is impossible to hope for the best case scenario. Even when \(f(A)=f(B)\), it might happen that the latent space is structured such that \(A\) and \(B\) are in different components of the level set of the function \(f\). Then there is no hope for a smooth hike without ups and downs! But the situation is not completely hopeless if we are fine with taking detours as long as such undesirables are minimized. We frame the problem as
$$\text{argmin}_{x_i \in L, \forall i} \sum_{i=1}^n |f(x_i) – f(B)|^2 + \lambda\sum_{i=1}^{n-2} |(x_{i+2}-x_{i+1}) – (x_{i+1} – x_i)|^2,
$$
where \(L\) is the latent space and \({x_i}_{i=1}^n\) is the sequence defining the path such that \(x_1 = A\) and \(x_n=B\). The first term is to encourage consistency in the function values, while the second term discourages sudden changes in curvature, thereby ensuring smoothness. Once defined, various gradient-based optimization algorithms can be used on this problem, which is now imposed with a relatively soft constraint.
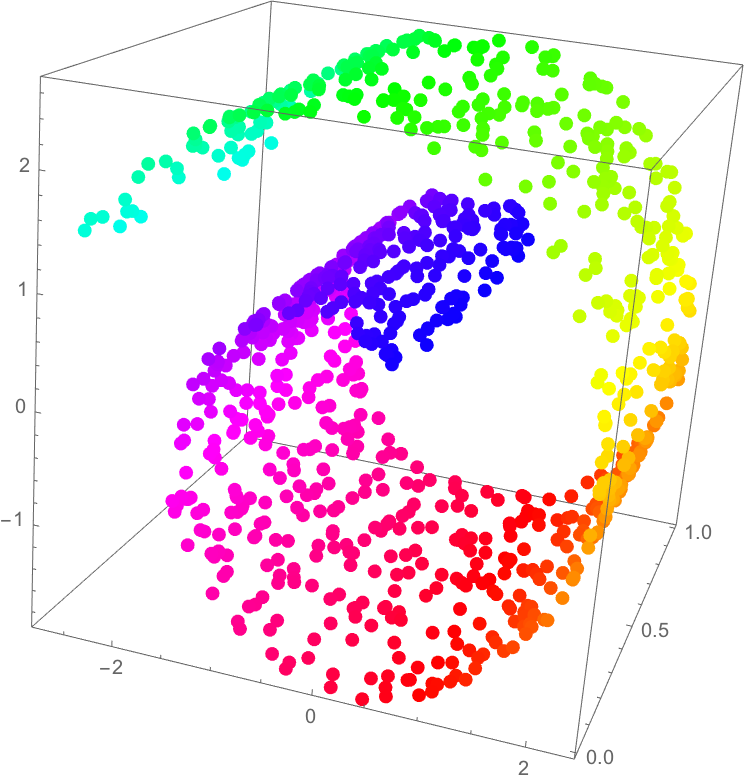
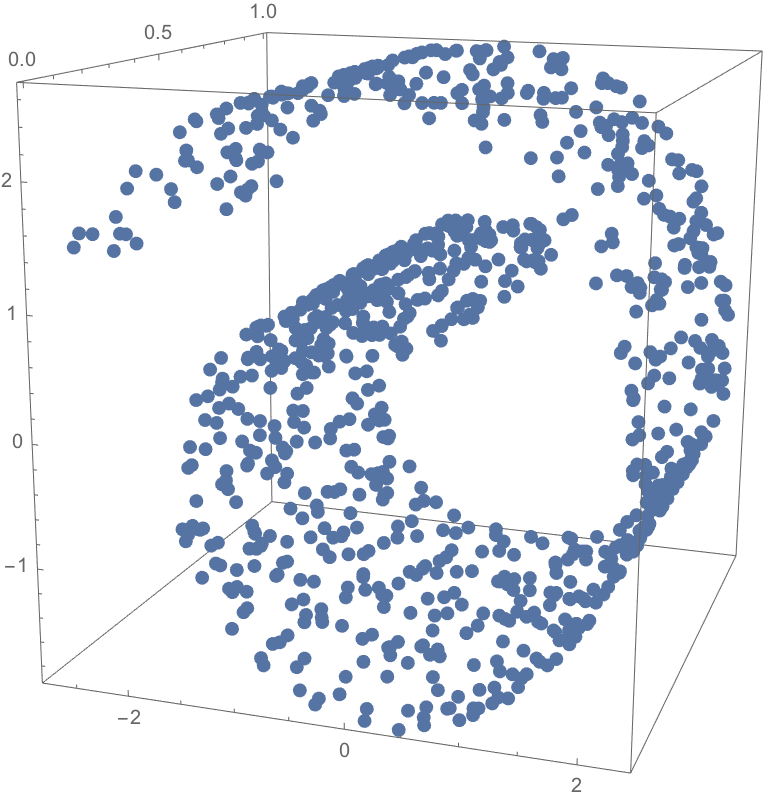
Results of pathfinding via optimization in different contexts.
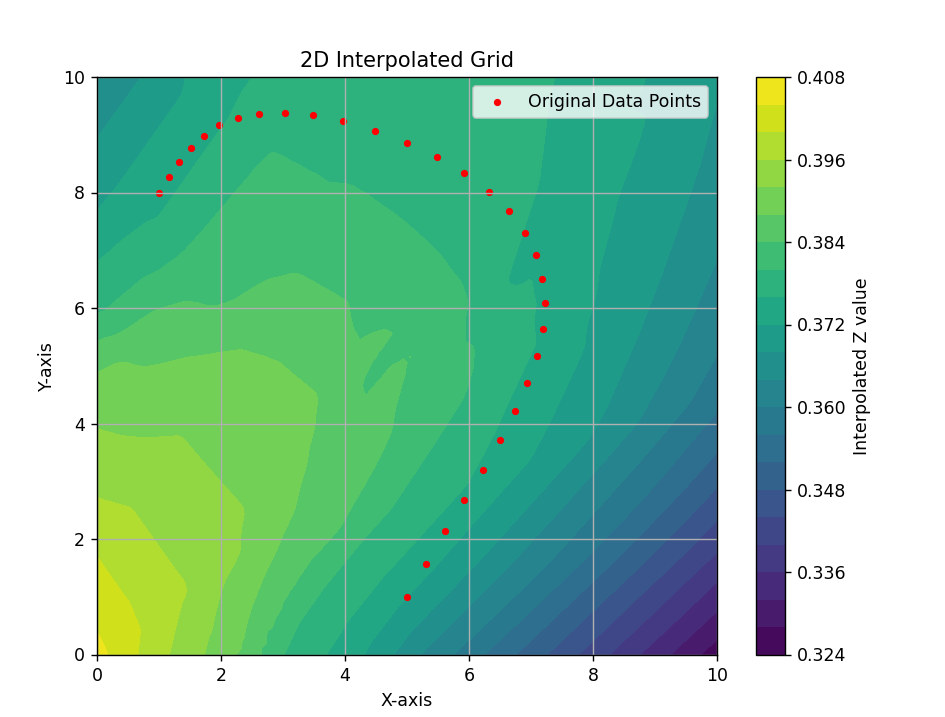
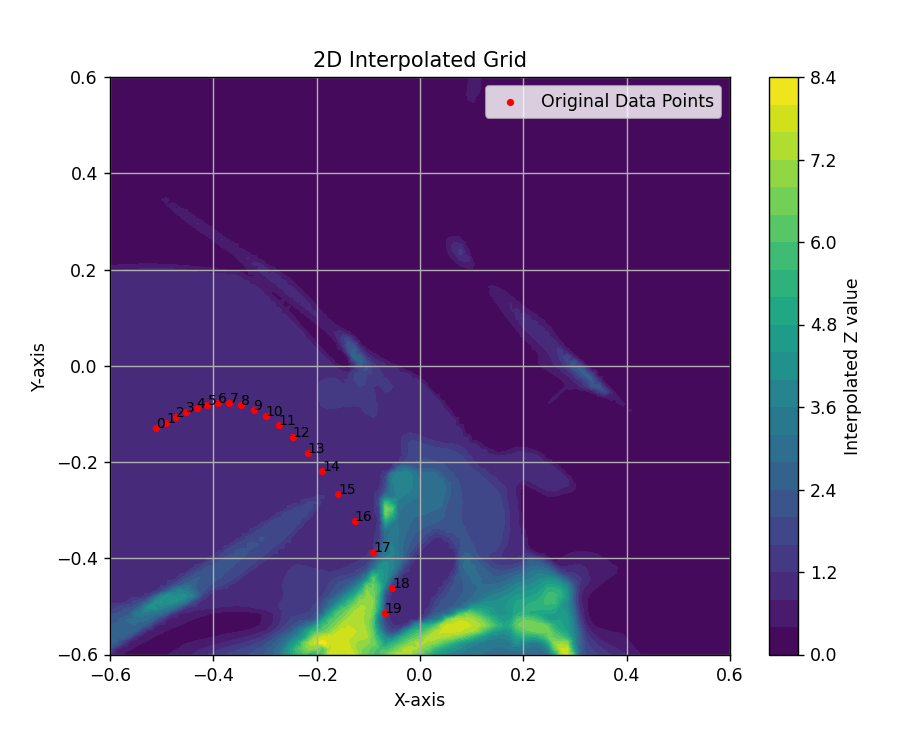
A Geodesic Path
One alternative attempt of note to optimize pathfinding used the concept of geodesics, or the shortest, smoothest distance between two points on a Riemannian manifold. In the latent space, one is really working over a latent data manifold, so thinking geometrically, we experimented with a geodesic path algorithm. In writing this algorithm, we set our two latent endpoints and optimized the points in between by minimizing the energy of our path on the output manifold. This alternative method worked similarly well to the optimized pathfinding algorithm posed above!
Conclusion and Future Work
Our journey into DeepSDFs, gradient methods, and geodesic paths has shown both the promise and the pitfalls of blending multiple specialized components. The decoupled design gave us flexibility, but also revealed a fragility—every part must share the same initialized latent space, and retraining one element (like the DeepSDF) forces a retraining of its companions, the regressor and classifier. With each component carrying its own error, the final solution sometimes felt like navigating with a slightly crooked compass.
Yet, these challenges are also opportunities. Regularization strategies such as Lipschitz constraints, eikonal terms, and Laplacian smoothing may help “tame” topological features, while alternative frameworks like diffeomorphic flows and persistent homology could provide more robust topological guarantees. The full integration of these models remains a work in progress, but we hope that this exploration sparks new ideas and gives you, the reader, a sharper sense of how topology can be preserved—and perhaps even mastered—in complex geometric learning systems.
Genus is a commonly known and widely applied shape feature in 3D computer graphics, but there is also a whole mathematical menu of topological invariants to explore along with their preservation techniques! Throughout our research, we also considered:
- Would topological accuracy benefit from a non-differentiable algorithm (e.g. RRT) that can directly encode genus as a discrete property? How would we go about certifying such an algorithm?
- How can homotopy continuation be used for latent space pathfinding? How will this method complement continuous deformations of homotopic and even non-homotopic shapes?
- What are some use cases to preserve topology, and what choice of topological invariant should we pair with those cases?
We invite all readers and researchers to take into account our struggles and successes in considering the questions posed.
Acknowledgements. We thank Professor Kry for his mentorship, Daria Nogina and Yuanyuan Tao for many helpful huddles, Professor Solomon for his organization of great mentors and projects, and the sponsors of SGI for making this summer possible.