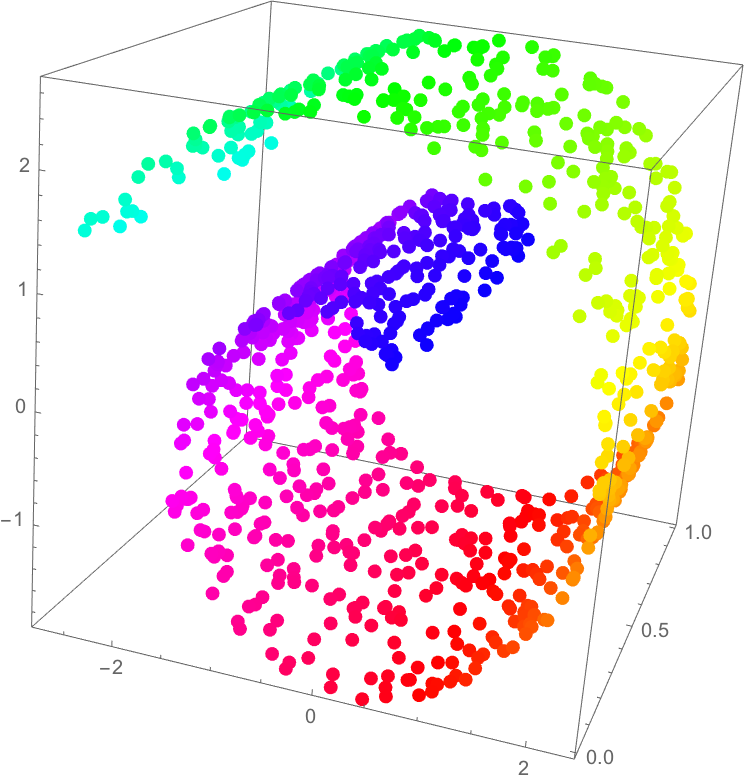
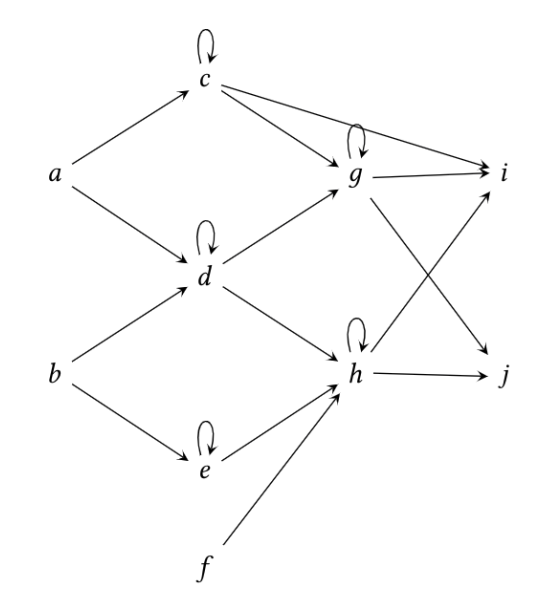
Quivers are a tool that are known to help us simplify problems in math. In particular, representations of quivers contribute to geometric perspectives in representation theory: the theory of reducing complex algebraic structures to simpler ones. Lesser known, neural networks can also be represented using quiver representation theory.
Fundamentally, a quiver is just a directed graph.
Intrinsic definitions to consider include:
- A source vertex of a quiver has no edges directed towards it
- A sink vertex has no edges directed away from it
- A loop in a quiver is an oriented edge such that the start vertex is the same as the end vertex
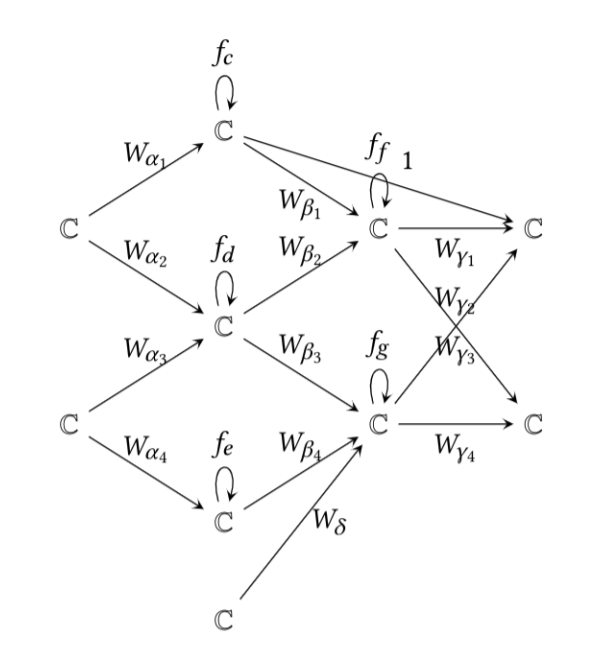
A fancy type of quiver known as an Auslander-Reiten quiver, courtesy of the author. But remember!, a quiver is simply a directed graph.
Just like an MLP, a network quiver \(Q\) is arranged by input, output, and hidden layers in between. Likewise, they also have input vertices (a subset of source vertices), bias vertices (the source vertices that are not input vertices), and output vertices (sinks of \(Q\)). All remaining vertices are hidden vertices. The hidden quiver \(\tilde{Q}\) consists of all hidden vertices \(\tilde{V}\) of \(Q\) and all oriented edges \(\tilde{E}\) between \(\tilde{V}\) of \(Q\) that are not loops.
Def: A network quiver \(Q\) is a quiver arranged by layers such that:
- There are no loops on source (input and bias) nor sink vertices.
- There exists exactly one loop on each hidden vertex
For any quiver \(Q\), we can also define its representation \(\mathcal{Q}\), in which we assign a vector space to each vertex of \(Q\) and regard our directed edges of \(Q\) as \(k\)-linear maps. In a thin representation, each \(k\)-linear map is simply a \(1\times1\) matrix.
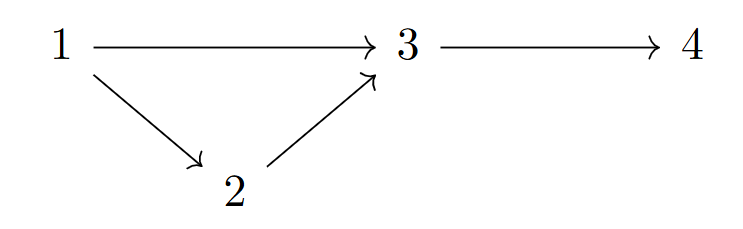
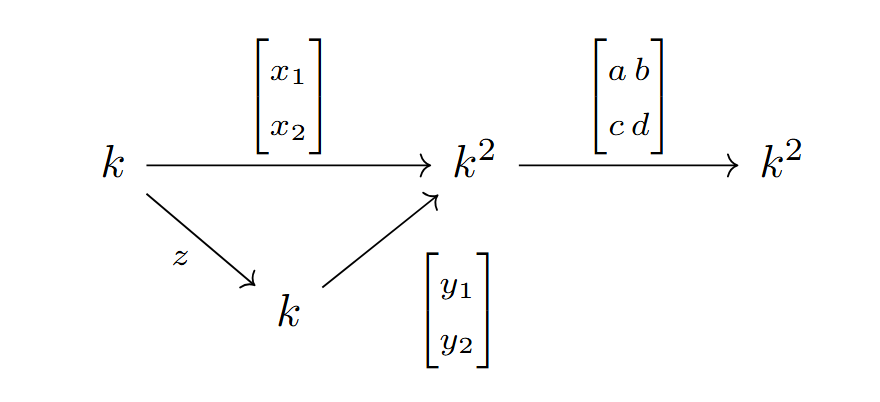
Defining a neural network \((W, f)\) over a network quiver \(Q\), where \(W\) is a specific thin representation and \(f = (f_v)_{v \in V}\) are activation functions, allows much of the language and ideas of quiver representation theory to carry over to neural networks .
When a neural network like an MLP does its forward pass, it gives rise to a pointwise activation function \(f\), defined here as a one variable non-linear function \(f: \mathbb{C} \to \mathbb{C}\) differentiable except in a set of measure zero. We assign these activation functions to loops of \(Q\).
Further, for a neural network \((W, f)\) over \(Q\), we have a network function
$$ \Psi(W, f): \mathbb{C}^d \to \mathbb{C}^k $$
where the coordinates of \(\Psi(W, f)(x)\) are the score of the neural net as the activation outputs of the output vertices of \((W, f)\) with respect to an input data vector \(x \in \mathbb{C}^d\).
The manifold hypothesis critical to deep learning proposes that high-dimensional data actually lies in a low-dimensional, latent manifold within the input space. We can map the input space to the geometric moduli space of neural networks \(_d\mathcal{M}_k(\tilde{Q})\) so that our latent manifold is also translated to the moduli space. While \(_d\mathcal{M}_k(\tilde{Q})\) depends on the combinatorial structure of the neural network, activation and weight architectures of the neural network determine how data is distributed inside the moduli space.
We will approach the manifold hypothesis via framed quiver representations. A choice of a thin representation \(\tilde{\mathcal{Q}}\) of the hidden quiver \(\tilde{Q}\) and a map \(h\) from the hidden representation \(\tilde{\mathcal{Q}}\) to hidden vertices determine a pair \((\tilde{\mathcal{Q}}, h)\), where \(h = \{h_v\}{v \in \tilde{V}}\). The pair \((\tilde{\mathcal{Q}}, h)\) is used to denote our framed quiver representation.
Def: A double-framed thin quiver representation is a triple \((l, \tilde{\mathcal{Q}}, h)\) where:
- \(\tilde{\mathcal{Q}}\) is a thin representation of the hidden quiver \(\tilde{Q}\)
- \((\tilde{\mathcal{Q}}, h)\) is framed representation of \(\tilde{Q}\)
- \((\tilde{\mathcal{Q}}, l)\) is a co-framed representation of \(\tilde{Q}\) (the dual of a framed representation)
Denote by \(_d\mathcal{R}_k(\tilde{\mathcal{Q}})\) the space of all double-framed thin quiver representations. We will use stable double-framed thin quiver representations in our construction of moduli space.
Def: A double-framed thin quiver representation \(\texttt{W}_k^f = (l, \tilde{\mathcal{Q}}, h)\) is stable if :
- The only sub-representation of \(\tilde{\mathcal{Q}}\) contained in the kernel of \(h\) is the zero sub-representation
- The only sub-representation of \(\tilde{\mathcal{Q}}\) contained in the image of \(l\) is \(\tilde{\mathcal{Q}}\)
Def: We present the moduli space of double-framed thin quiver representations as
$$ _d\mathcal{M}_k(\tilde{Q}):=\{[V]: _d\mathcal{R}_k(\tilde{\mathcal{Q}}) \space \text{is stable} \}. $$
The moduli space depends on the hidden quiver as well as the chosen vector spaces. Returning to neural networks \((W, f)\), and given an input data vector \(x \in \mathbb{C}^d\), we can define a map
$$ \varphi(W, f): \mathbb{C}^d \to _d\mathcal{R}_k(\tilde{\mathcal{Q}})\\x \mapsto \texttt{W}_k^f. $$
This map takes values in the moduli space, the points of which parametrize isomorphism classes of stable double-framed thin quiver representations. Thus we have
$$ \varphi(W, f): \mathbb{C}^d \to _d\mathcal{M}_k(\tilde{Q}).
$$
As promised, we have mapped our input space containing our latent manifold to the moduli space \(_d\mathcal{M}_k(\tilde{Q})\) of neural networks, mathematically validating the manifold hypothesis.
Independent of the architecture, activation function, data, or task, any decision of any neural network passes through the moduli (as well as representation) space. With our latent manifold translated into the moduli space, we have an algebro-geometric way to continue to study the dynamics of neural network training.
Looking through the unsuspecting the lens of quiver representation theory has the potential to provide new insights in deep learning, where network quivers appear as a combinatorial tool for understanding neural networks and their moduli spaces. More concretely:
- Continuity and differentiability of the network function \(\Psi(W, f)\) and map \(\varphi(W, f)\) should allow us to apply further algebro-geometric tools to the study of neural networks, including to our constructed moduli space \(_d\mathcal{M}_k(\tilde{Q})\).
- Hidden quivers can aid us in comprehending optimization hyperparameters in deep learning. We may be able to transfer gradient descent optimization to the setting of the moduli space.
- Studying training within moduli spaces can lead to the development of new convergence theorems to guide deep learning.
- The dimension of \(_d\mathcal{M}_k(\tilde{Q})\) could be used to quantify the capacity of neural networks.
The manifold hypothesis has played a ubiquitous role throughout deep learning since originally posed, and formalizing its existence via the moduli of quiver representations can help us to understand and potentially improve upon the effectiveness of neural networks and their latent spaces.
Notes and Acknowledgements. Content for this post was largely borrowed from and inspired by The Representation Theory of Neural Networks, smoothing over many details more rigorously presented in the original paper. We thank the 2025 SGI organizers and sponsors for supporting the author’s first deep learning-related research experience via the “Topology Control” project as well as mentors and other research fellows involved for their diverse expertise and patience.