Tag: mesh fairing

Categories
Tutorial week

Ironing Out Wrinkles with Mesh Fairing

Picture your triangle mesh as that poor, crumpled T-shirt you just pulled out of the dryer. It’s full of sharp folds, uneven patches, and you wouldn’t be caught dead wearing it in public—or running a physics simulation! In geometry processing, these “wrinkles” manifest as skinny triangles, janky angles, and noisy curvature that spoil rendering, break solvers, or just look… ugly. Sometimes, we might want to fix these problems using something geometry nerds call surface fairing.

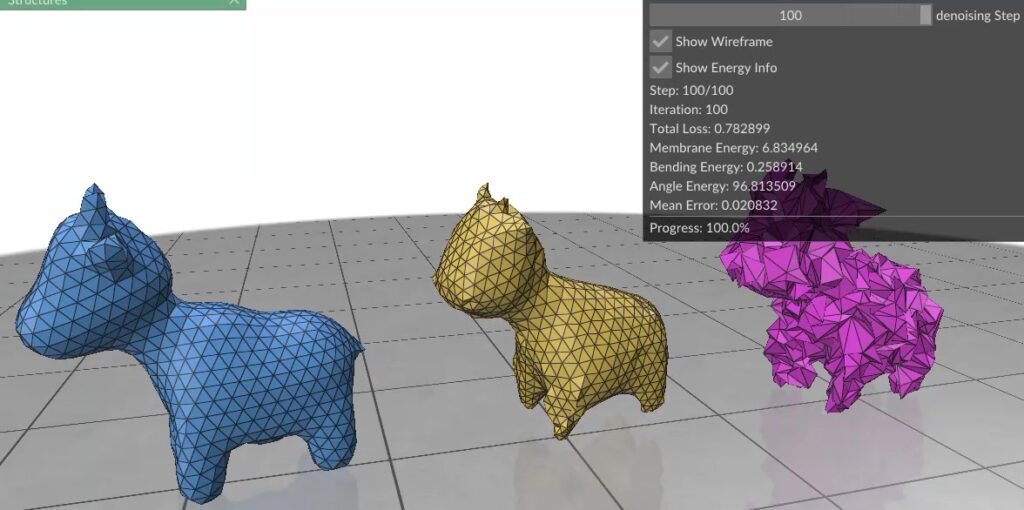
Figure 1. (Left) Clean mesh, (Right) Mesh damaged by adding Gaussian noise to each vertex (Middle) Result after applying surface fairing to the damaged mesh.

In essence, surface fairing is an algorithm one uses to smoothen their mesh. Surface fairing can be solved using energy minimization. We define an “energy” that measures how wrinkly our mesh is, then use optimization algorithms to slightly nudge each vertex so that the total energy drops.

  1. Spring Energy
    Think of each mesh edge (i,j) as a spring with rest length 0. If a spring is too long, it costs energy. Formally:
    Emem = ½ Σ(i,j)∈E wij‖xi − xj‖² with weights wij uniform or derived from entries of the discrete Laplacian matrix (using cotangents of opposite angles). We’ll call this term the Membrane Term
  2. Bending Energy
    Sometimes, we might want to additionally smooth the mesh even if it looks less wrinkly. In this case, we penalize the curvature of the mesh, i.e., the rate at which normals change at the vertices:
    Ebend = ½ Σi Ai‖Δxi‖² where Δxi is the discrete Laplacian at vertex i and Ai is its “vertex area”. For the uninitiated, the idea of a vertex having an area might seem a little weird. But it represents how much area a vertex controls and is often calculated as one-third of the summed areas of triangles incident to vertex i. We’ll call this energy term the Laplacian Term.
  3. Angle Energy
    As Nicholas has warned the fellows, sometimes, having long skinny triangles can cause numerical instability. So we might like our triangles to be more equilateral. We can additionally punish deviations from 60° for each triangle, by adding another energy term: Eangle = Σk=1..3(θk−60°)². We’ll call this the Angle Term.
Figure 2. (Left) Damaged mesh. (In order) Surface fairing using only 1) Spring Energy 2) Bending Energy 3) Angle Energy. Notice how the last two energy minimizations fail to smooth the mesh properly alone.

Note that in most cases using angle energy and bending energy terms are optional, but using the spring energy term is important! (however, you may encounter a few special cases where you can make do without the spring energy?? i’m not too sure, don’t take my word for it). Once we have computed these energies, we weight them appropriately with scaling factors and sum them up. The next step is to minimize them. I love Machine Learning and hate numerical solvers; and so, it brings me immense joy to inform you that since the problem is non-convex, we can should use gradient descent! At each vertex, compute the gradient ∇xE and take a tiny step towards the minima: \(x_{i} \leftarrow x_i – \lambda \cdot (\nabla_{x} E)_{i}\)

Now, have a look at our final surface fairing algorithm in its fullest glory. Isn’t it beautiful? Maybe you and I are nerds after all 🙂

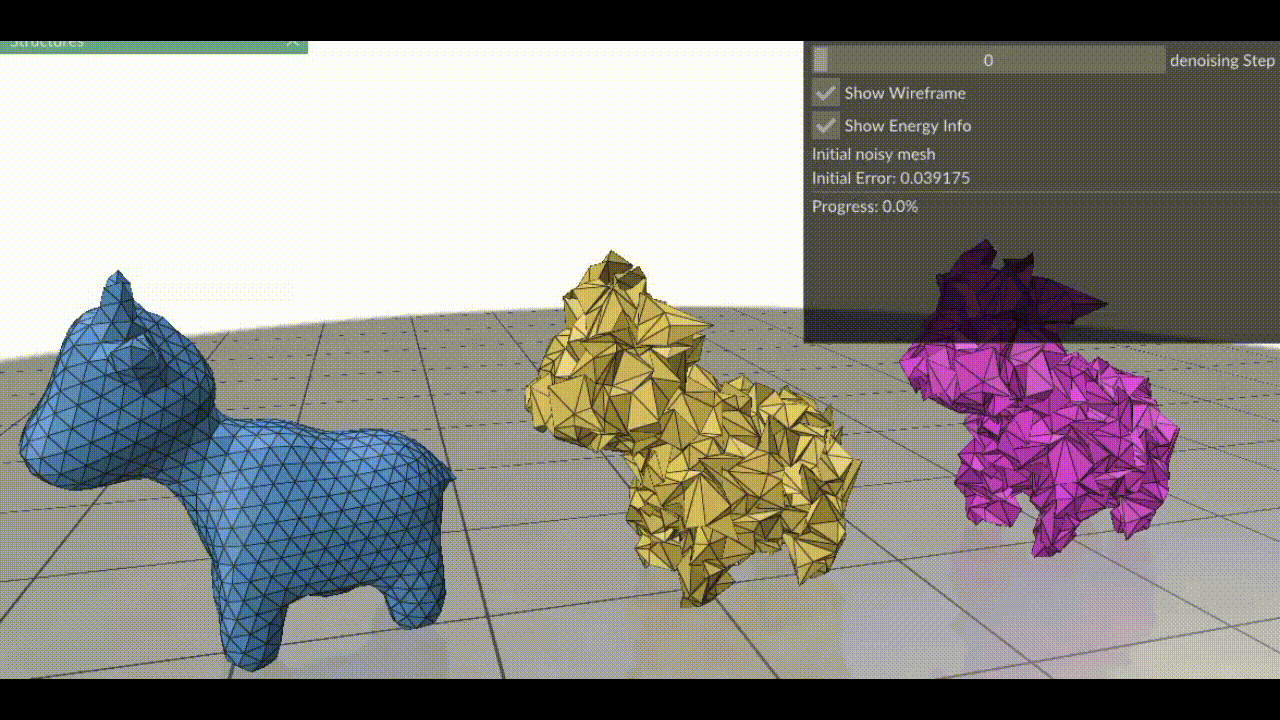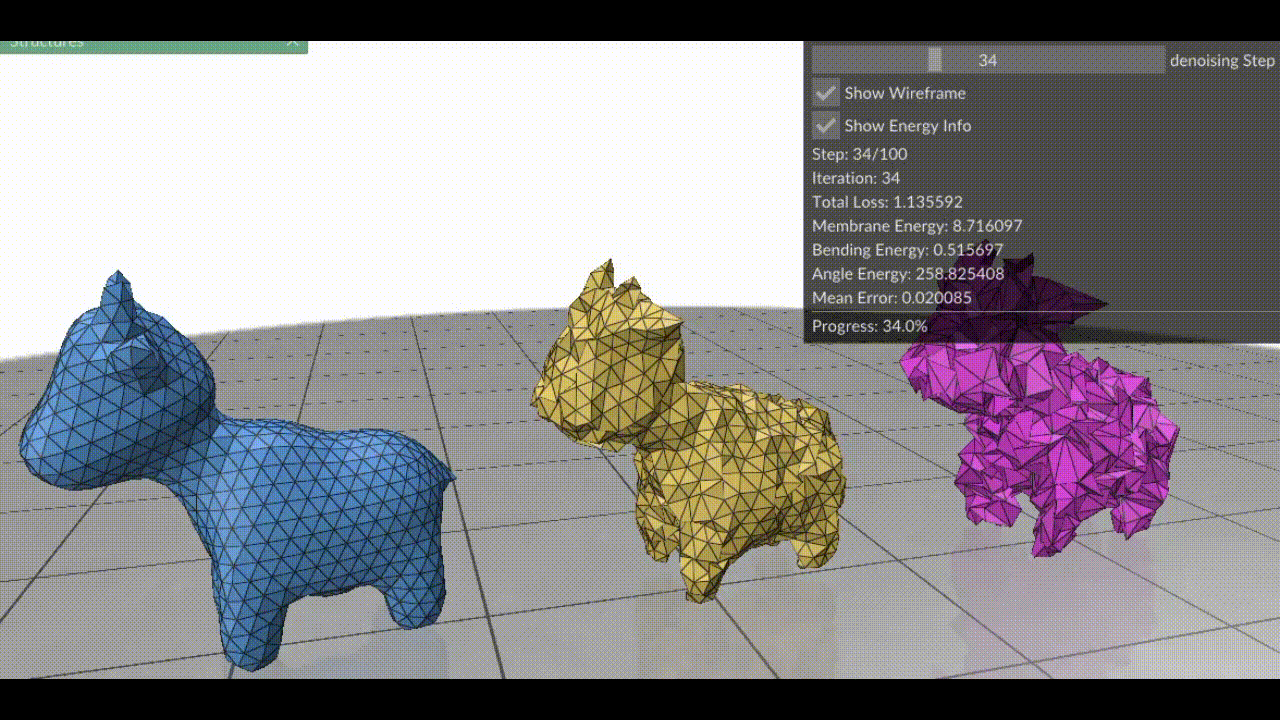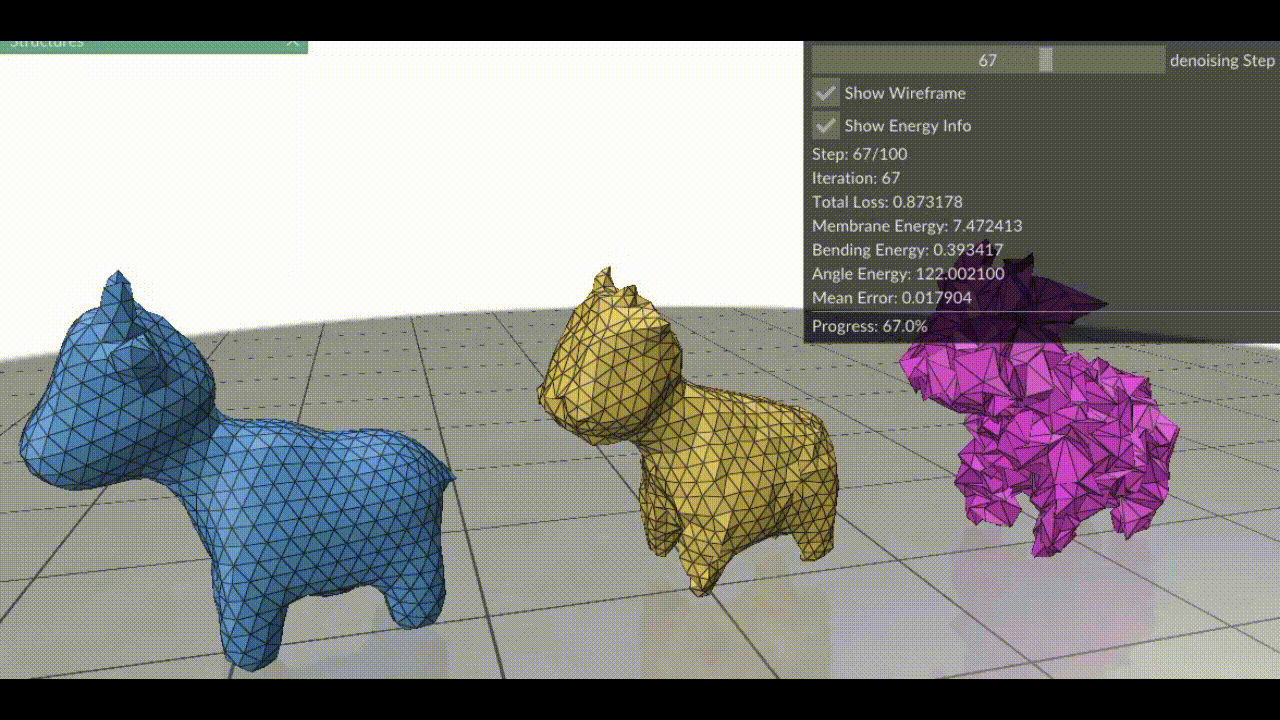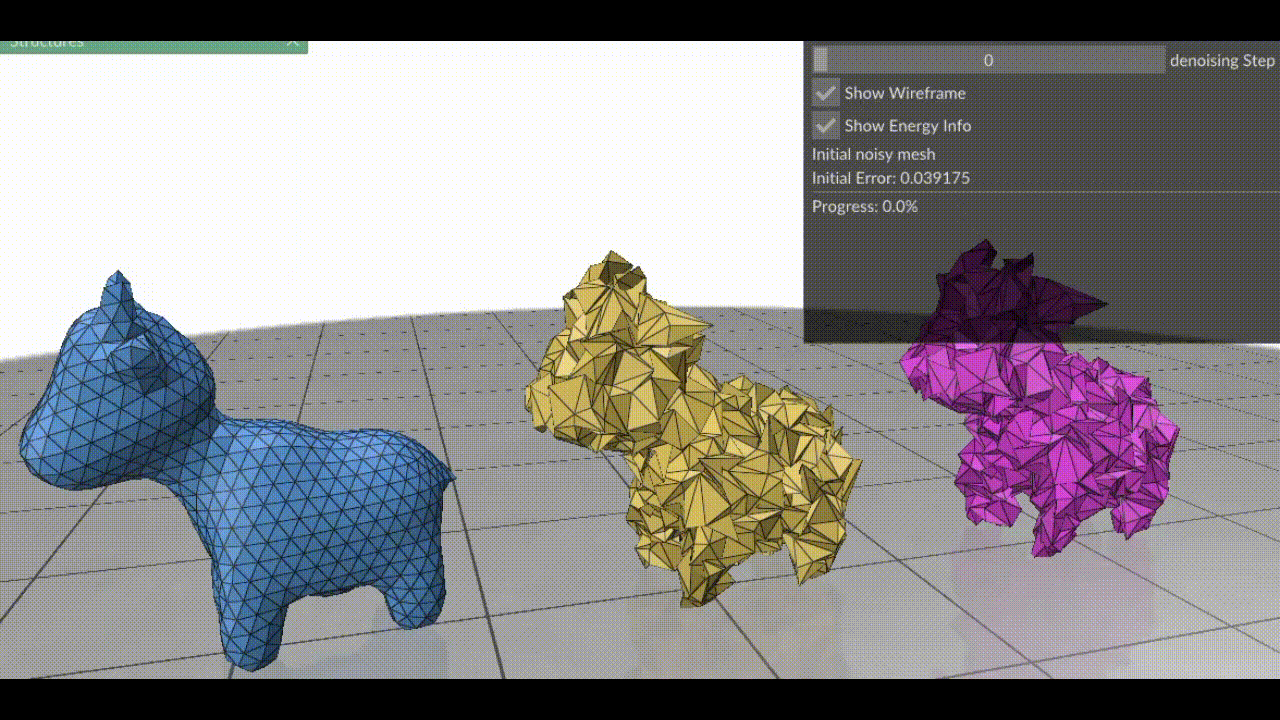
Figure 1. (Left) Clean mesh, (Right) Damaged mesh (Middle) Resulting mesh after each step of gradient descent on the three energy terms combined. Note how the triangles in this case are more equilateral than the red mesh in Figure 2, because we’ve combined all energy terms.

So, the next time your mesh looks like you’ve tossed a paper airplane into a blender, remember: with a bit of math and a few iterations, you can make it runway-ready; and your mesh-processing algorithm might just thank you for sparing its life. You can find the code for the blog at github.com/ShreeSinghi/sgi_mesh_fairing_blog.

Happy geometry processing!

References

  • Desbrun, M., Meyer, M., Schröder, P., & Barr, A. H. (1999). Implicit fairing of irregular meshes using diffusion and curvature flow.
  • Pinkall, U., & Polthier, K. (1993). Computing discrete minimal surfaces and their conjugates.