By Ruyu Yan, Xinyi Zhang
Invariant Point Cloud Classification
We experimented with incorporating SE(3) invariance into a point cloud classification model based on our prior study on Frame Averaging for Invariant and Equivariant Network Design. We used a simple PointNet architecture, dropping the input and feature transformations, as our backbone.
Method and Implementation
Similar to the normal estimation example provided in the reference paper, we defined the frames to be
\(\mathcal{F}(X)=\{([\alpha_1v_1, \alpha_2v_2, \alpha_3v_3], t)|\alpha_i\in\{-1, 1\}\}\subset E(3) \)
where \(\mathbb{t}\) is the centroid and \(v_1, v_2, v_3\) are the principle components of the point cloud \(X\). Then, we have the frame operations
\(\rho_1(g)=\begin{pmatrix}R &t \\0^T & 1\end{pmatrix}, R=\begin{bmatrix}\alpha_1v_1 &\alpha_2v_2&\alpha_3v_3\end{bmatrix} \)
With that, we can symmetrize the classification model \(\phi:V \rightarrow \mathbb{R}\) by
\(\langle \phi \rangle \mathcal{F}(X)=\frac{1}{|\mathcal{F}(X)|}\sum_{g\in\mathcal{F}(X)}\phi(\rho_1(g)^{-1}X) \)
Here we show the pseudo-code of our implementation of the symmetrization algorithm in the forward propagation through the neural network. Please refer to our first blog about this project for details on get_frame and apply_frame functions.
def forward(self, pnt_cloud):
# compute frames by PCA
frame, center = self.get_frame(pnt_cloud)
# apply frame operations to re-centered point cloud
pnt_cloud_framed = self.apply_frame(pnt_cloud - center, frame)
# extract features of framed point cloud with PointNet
pnt_net_feature = self.pnt_net(pnt_cloud_framed)
# predict likelihood of classification to each category
pred_scores = self.classify(pnt_net_features)
# take the average of prediction scores over the 8 frames
pred_scores_averaged = pred_scores.mean()
return pred_scores_averaged
Experiment and Comparison
We chose Vector Neurons, a recent framework for invariant point cloud processing, as our experiment baseline. By extending neurons from 1-dimensional scalars to 3-dimensional vectors, the Vector Neuron Networks (VNNs) enable a simple mapping of SO(3) actions to latent spaces and provide a framework for building equivariance in common neural operations. Although VNNs could construct rotation-equivariant learnable layers of which the actions will commute with the rotation of point clouds, VNNs are not very compatible with the translation of point clouds.
In order to build a neural network that commutes with the actions of the SE(3) group (rotation + translation) instead of the actions of the SO(3) group (rotation only), we will use Frame Averaging to construct the equivariant autoencoders that are efficient, maximally expressive, and therefore universal.
Following the implementation described above, we trained a classification model on 5 selected classes (bed, chair, sofa, table, toilet) in the ModelNet40 dataset. We obtained a Vector Neurons classification model with the same PointNet backbone (input and feature transformation included) pre-trained on the complete ModelNet40 dataset. We tested the classification accuracy on both models with point cloud data of the 5 selected classes randomly transformed by rotation-only or rotation and translation. The results are shown in the table below.
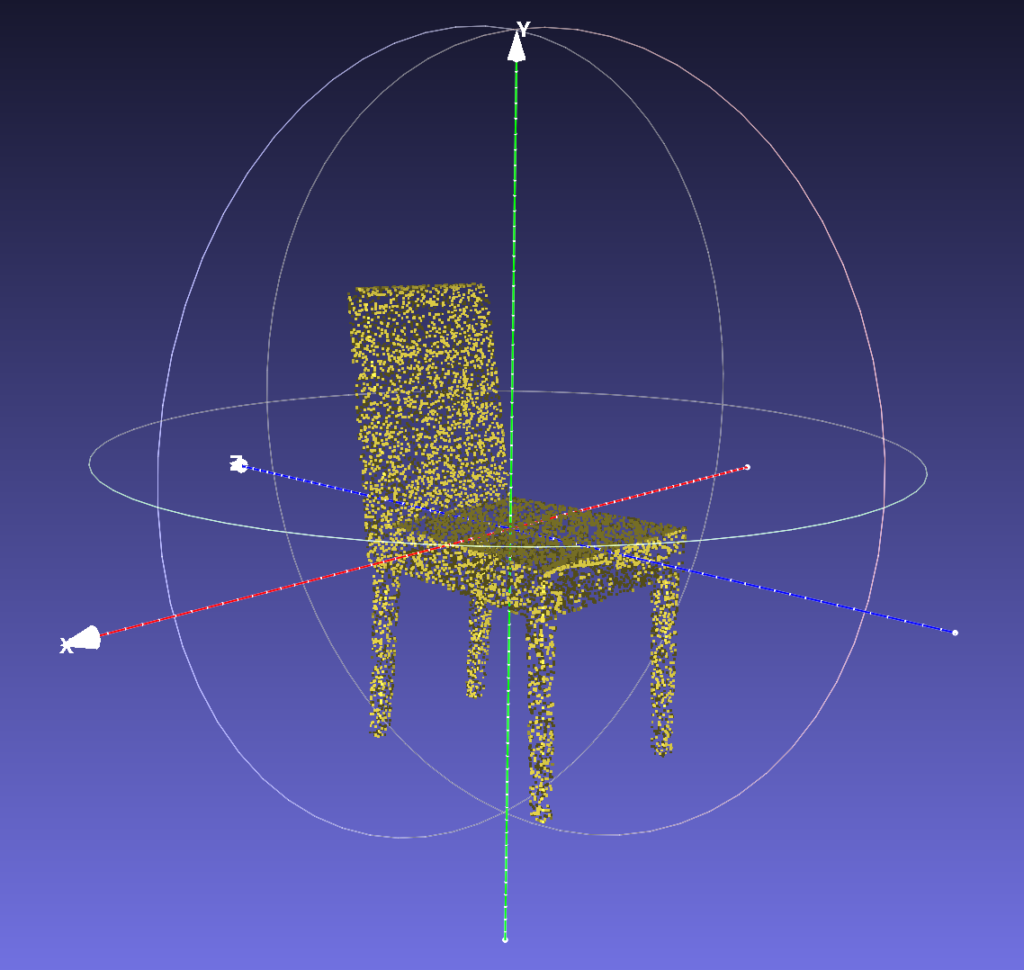
| SO(3) Test Instance Accuracy | SE(3) Test Instance Accuracy | |
| Vector Neurons | 89.6% | 6.1% |
| Frame Averaging | 80.7% | 80.3% |
The Vector Neurons model was trained for a more difficult classification task, but it was also more fined tuned with a much longer training time and larger data size. The Frame Averaging model in our experiment, however, was trained with relatively larger learning steps and shorter training time. Although it is not fair to make a direct comparison between the two models, we can still see a conclusive result. As expected, the Vector Neurons model has good SO(3) invariance, but tends to fail when the point cloud is translated. The Frame Averaging model, on the other hand, performs similarly well on both SO(3) and SE(3) invariance tests.
If the Frame Averaging model was trained with the same setting as the Vector Neurons model, we believe that it will have both the accuracy of SO(3) and SE(3) tests comparable with Vector Neurons’ SO(3) accuracy, because of its maximal expressive power. Due to the limited resource, we cannot prove our hypothesis by experience, but we will provide more theoretical analysis in the next section.
Discussion: Expressive Power of Frame Averaging
Besides the good performance in maintaining SE(3) invariance in classification tasks, we want to further discuss the advantage of frame averaging, namely its ability to preserve the expressive power of any backbone architecture.
The Expressive Power of Frame Averaging
Let \(\phi: V \rightarrow \mathbb{R}\) and \(\Phi: V \rightarrow W\) be some arbitrary functions, e.g. neural networks where \(V, W\) are normed linear spaces. Let \({G}\) be a group with representations \(\rho_1: G \rightarrow GL(V)\) and \(\rho_2: G \rightarrow GL(W)\) that preserve the group structure.
Definition
A frame is bounded over a domain \(K \subset V\) if there exists a constant \(c > 0\) so that \(||\rho_2(g)|| \leq c\) for all \(g \in F(X)\) and all \(X \in K\) where \(||\cdot||\) is the operator norm over \(W\).
A domain \(K \subset V\) is frame finite if for every \(X \in K\), \(F(X)\) is a finite set.
A major advantage of Frame Averaging is its preservation of the expressive power of the base models. For any class of neural networks, we can see them as a collection of functions \(H \subset C(V,W)\), where \(C(V,W)\) denotes all the continuous functions from \(V\) to \(W\). We denote \(\langle H \rangle = \{ \langle \phi \rangle | \phi \in H\}\) as the transformed \(H\) after applying the frame averaging. Intuitively, the expressive power tells us the approximation power of \(\langle H \rangle\) in comparison to \(H\) itself. The following theorem demonstrates the maximal expressive power of Frame averaging.
Theorem
If \(F\) is a bounded \(G\)-equivariant frame over a frame-finite domain \(K\), then for any equivariant function \(\psi \in C(V,W)\), the following inequality holds
\(\inf_{\phi \in H}||\psi – \langle \phi \rangle_F||{K,W} \leq c \inf{\phi \in H}||\psi – \phi||_{K_F,W} \)
where \(K_F = \{ \rho_1(g)^{-1}X | X \in K, g \in F(X)\}\) is the set of points sampled by the FA operator and $c$ is the constant from the definition above.
With the theorem above, we can therefore prove the universality of the FA operator. Let \(H\) be any collection of functions that are universal set-equivariant, i.e., for arbitrary continuous set function \(\psi\) we have \(\inf_{\phi \in H} ||\psi – \phi||_{\Omega,W} = 0\) for arbitrary compact sets \(\Omega \subset V\). For bounded domain \(K \subset V\), \(K_F\) defined above is also bounded and contained in some compact set \(\Omega\). Therefore, we can conclude with the following corollary.
Corollary
Frame Averaging results in a universal SE(3) equivariant model over bounded frame-finite sets, \(K \subset V\).