By: Caroline Huber, Natalie Patten, and Xinyi Zhang
On August 1st we began working on a project titled: “Tight Isoperimetric Profiles” mentored by Richard Barnes of the Lawrence Berkeley National Lab and Michigan State University PhD student Erik Amezquita.
We began the first week by looking at “Medial Axis Isoperimetric Profiles” (Zhang, DeFord, & Solomon, 2020). We read this alongside excerpts from provided materials, such as: Skiena’s “The Algorithm Design Manual” and Garey and Johnson’s “Computers and Intractability.”
Initial code was used to replicate the findings of “Medial Axis Isoperimetric Profiles” and to use this to extrapolate our own algorithm. The figure below shows the computation of the medial axis of a shape from the aforementioned code.
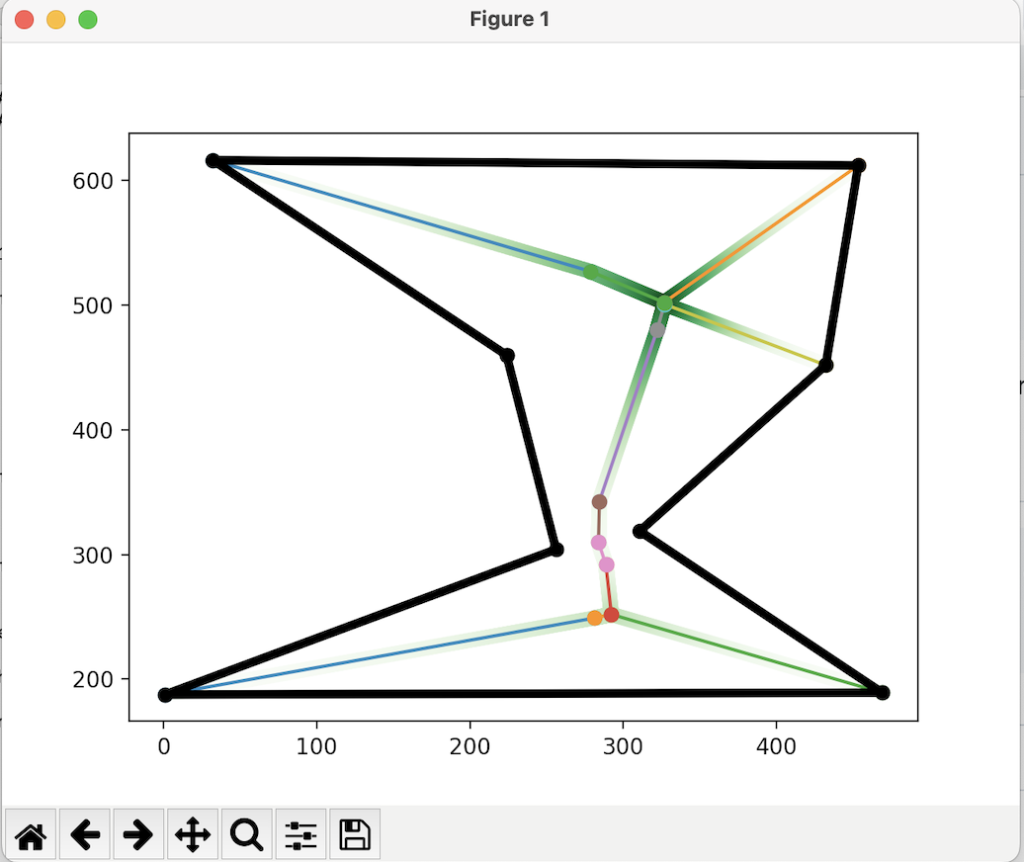
The isoperimetric ratio (\(\frac{4\pi*A}{p^2}\)) of a shape with perimeter \(p\) and area \(A\) measures the compactness of said shape. To maximize the area and limit the perimeter of a shape, one would look for a shape with a high isoperimetric profile (the highest being a circle with a score of 1.0). However, for shapes with boundary perturbation, the ratio is unstable; hence the isoperimetric profile is used instead: \(IP_{\Omega}(t):=min\{length({\partial}F): F\subseteq\Omega \& area(F)=t\}\).
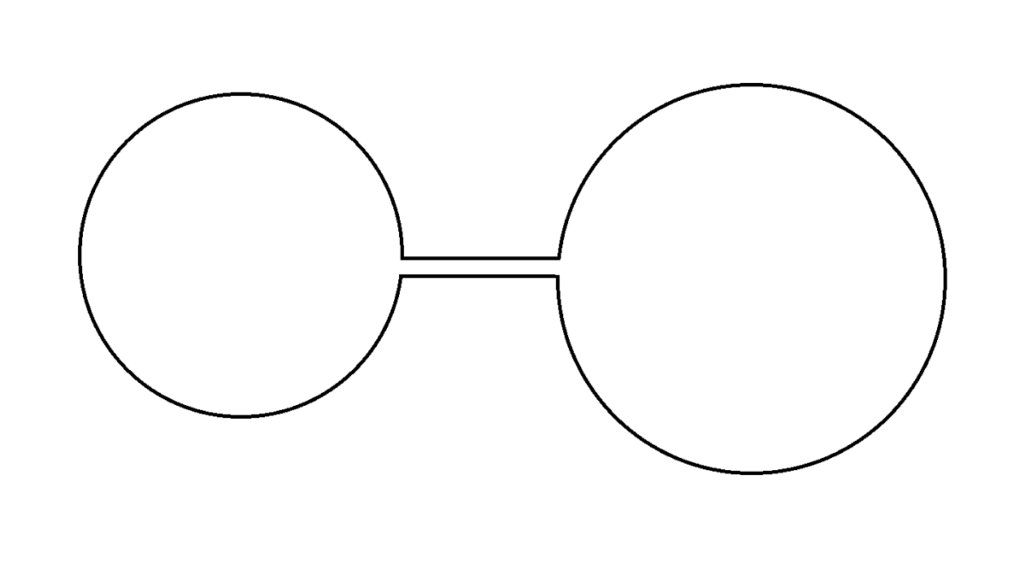
Currently, only brute-force methods exist for calculating isoperimetric profiles (IPs) of shapes with thin necks. Recent research, published in “Medial Axis Isoperimetric Profiles” has created a less expensive algorithm for computing IPs of shapes with thick necks, utilizing the concept of medial axes and graph nodes. By applying a greedy traversal along the medial axis of 2D shapes, this algorithm provides a tight bound for IPs of shapes with thick necks. However, the greedy traversal of adjacent nodes fails to provide a tight bound for IPs of shapes with thin necks. For example, Figure 2 is a clear illustration of the failure of the greedy traversal of adjacent nodes. In this case, the greedy traversal fails to capture the information of the large circle on the other side of the dumbbell due to the existence of a thin neck.
Thus, we have expanded on this research and revised the algorithm to formulate our proposed algorithm for shapes with thin necks. An overview of the algorithm-along with germane nomenclature-can be viewed below:

To solve the problems created by the thin necks, we will partition the whole shape into different components according to its thin necks and define this new set of points as the set of centers of the largest circles in each component as \(L\). We will now apply the greedy algorithm not only to the adjacent points but also to the points in \(L\). In this way, we can solve the problems that cannot be solved by the original algorithm in cases like Figure 2 by capturing and encoding the information of the large circles on the other side of the thin necks in this \(L\) set.
Some problems we anticipate this algorithm may encounter include:
- Shapes with many thin necks
- Shapes with different size “openings” on either side of its thin neck(s)
We enjoyed working on this project and learning about isoperimetric profiles and the current research being done in this area. We also enjoyed learning about the different potential applications of this research–for example, to examine possible gerrymandering.