SGI Fellows: Harini Rammohan, Nicolas Pigadas, Riccardo Ali
Project Mentors: Mahdi Saleh and Dani Velikova
SGI Volunteer: Matheus Araujo
Optimal Transport and the Sinkhorn Algorithm:
Optimal Transport (OT), intuitively speaking, finds the most efficient way to transport mass from one probability distribution to another. For example, suppose the surface of a beach is given as the ambient space \(X\), and the various distributions of sand on the surface are represented by probability distributions on \(X\). Suppose also that we are given a cost function \(C:X\times X\to\mathbb{R}_{\geq 0} \), where \(C(x,y)\) represents the cost of moving a unit mass of sand from point \(x\) to point \(y\). The OT problem in this setting is to move the sand from a source distribution to a target distribution while minimizing the total transportation cost. Working with continuous distributions is often not feasible computationally, so a common approach is to discretize distributions, say by dividing the beach into a finite collection of bins and extracting an optimal transport plan for moving sand amongst this finite collection.
In the discrete case, the transportation cost can represented by a cost matrix \(C\), where \(C_{i,j}\) is the cost of moving a unit mass of sand from bin \(i\) to bin \(j\). The Wasserstein distance between two distributions is defined as the transportation cost for the minimal transport plan and can be obtained via the Sinkhorn Algorithm. Sinkhorn’s theorem states that if \(A\) is a square matrix with positive entries, then there exist two diagonal matrices \(D_1\) and \(D_2\) with positive diagonal entries such that \(T = D_1AD_2\) is doubly stochastic (all rows and columns sum to 1). The algorithm recursively rescales rows and columns of the input matrix A until it converges to the required matrix \(T\). \(T_{ij}\) returns the amount of mass that must be transported from bin \(i\) to bin \(j\) in the minimal transport plan.
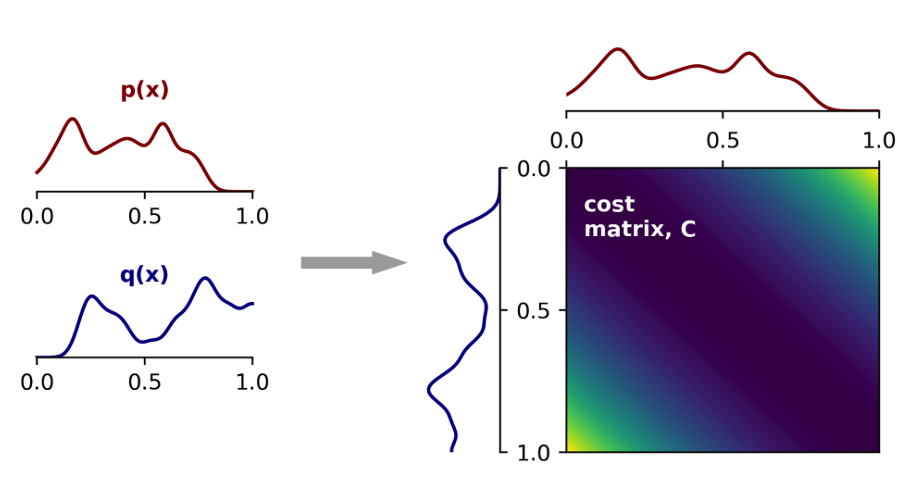
Image from https://alexhwilliams.info/itsneuronalblog/2020/10/09/optimal-transport/
6D Pose Estimation using the Sinkhorn Solver:
6D pose estimation refers to the process of determining the position and orientation (together called the pose) of an object (CAD) in a three-dimensional space from an image of that object. Seeing pixels as bins and pixel values as the mass of sand in that bin, the Sinkhorn algorithm can be used to find a transport plan for matching pixels in the image to points in \(\mathbb{R}^3\). However, if the object is symmetric, there may be ambiguity in its pose and one could get multiple poses that match the image. In this case, the standard Sinkhorn approach fails. Inspired by the work in the SuperGlue {1} and EPOS {2} papers, we aimed to extend the differentiable Sinkhorn solver to cases with one-to-many solutions and incorporate graph neural networks to estimate the 6D pose of such symmetric objects.
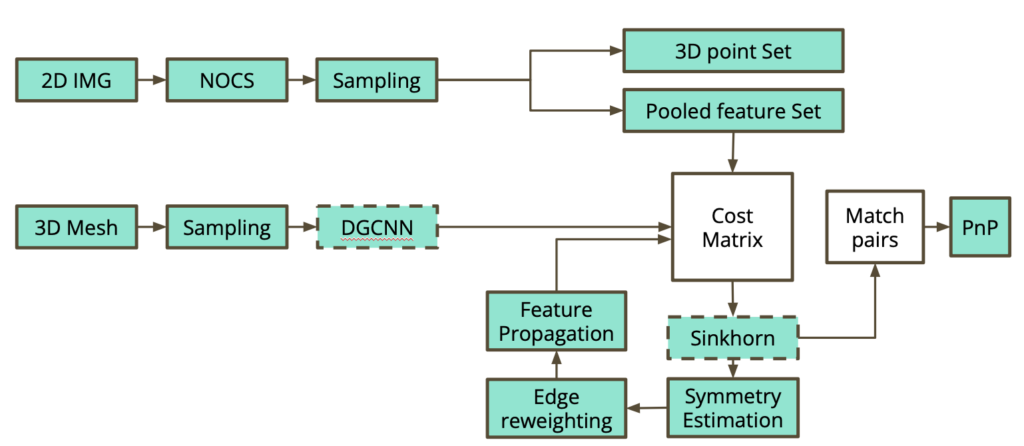
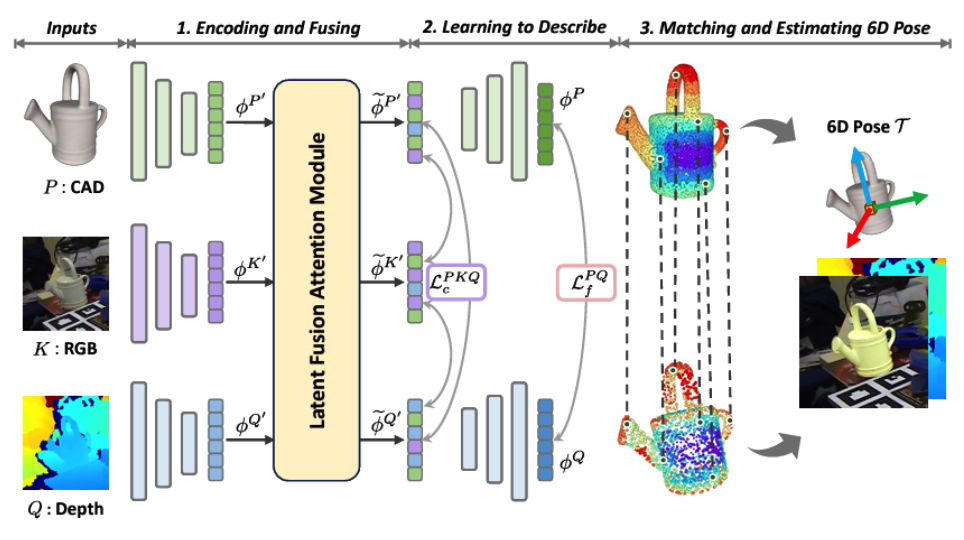
Image from Huang, Junwen, et al. “Matchu: Matching unseen objects for 6d pose estimation from rgb-d images.”CVPR. 2024
The hurdles were, first to come up with a cost matrix that best suited the problem, implement a one-to-many Sinkhorn solver from the Python OT library, and use a Perspective-N-Point {5} approach to find the pose of each of the solutions returned by the Sinkhorn solver. Another challenge was finding the correct axis of symmetry of the pose; we planned to first assume prior information about the axis of symmetry and later incorporate the problem of finding this axis itself. Unfortunately, we decided not to continue with the second week of the project and hence were not able to produce concrete results. However, a brief description of our ideas for overcoming each hurdle is given below.
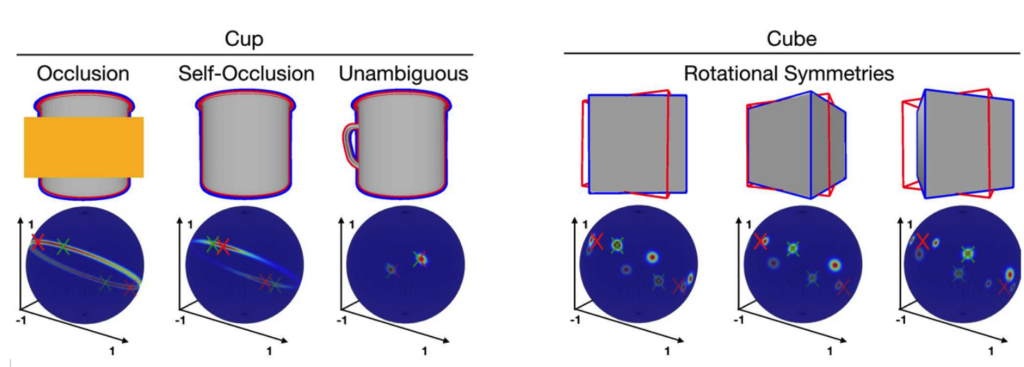
Image from Manhardt, Fabian, et al. “Explaining the ambiguity of object detection and 6d pose from visual data.” ICCV 2019.
Ideas for the Implementation:
The image was meant to be a 2D point cloud with features from which we could determine a partial 3D point cloud. One idea we had for the cost matrix, in the case where the axis of symmetry is known, was to add a symmetry-aware cost to reduce the cost for matches that are consistent with the given symmetry. We could also try to find the translation vector by inferring it from points on the axis of symmetry of the CAD and the corresponding matches in the image. Once we do this, we will have to deal with the rotation vector, which can be optimized separately using the Sinkhorn algorithm.
The special Euclidean group (SE(3)) is the group of all combinations of rotations, reflections, and translations in \(\mathbb{R}^3\). If we have no information about the axis of symmetry, then this group forms the set of all possible 6D poses. In this case, we must find poses in SE(3) that minimize transportation costs. We could try to compare images of the CAD after applying a pose and the 2D image point cloud and reduce the distance between the two to find the possible poses of the image.
One approach to extend the existing Sinkhorn solver to get multiple solutions is first to use the existing one to get a single solution, and then find all transport matrices that have a similar cost to the one obtained. Another is to design a collection of cost matrices rather than a single one, in a way that the existing Sinkhorn solver produces multiple (and hopefully all) possible solutions. We could get this collection of matrices by applying various poses to the original CAD as before and compute the cost of going from the modified CADs to the image.
Acknowledgements:
During the one week of the project, I learned so much about optimal transport, image matching, and pose estimation. I am very grateful to our mentors who supported and guided our progress.
References:
{1} Sarlin, Paul-Edouard, et al. “SuperGlue: Learning Feature Matching with Graph Neural Networks.” CVPR, 2020, https://doi.org/10.48550/arXiv.1911.11763.
{2} Hodan, Tomas, et al. “EPOS: Estimating 6D Pose of Objects with Symmetries.” CVPR, 2020, https://doi.org/10.48550/arXiv.2004.00605.
{3} Drost, Bertram, et al. “Explaining the Ambiguity of Object Detection and 6D Pose From Visual Data.”, ICCV, 2019, https://doi.org/10.48550/arXiv.1812.00287
{4} Williams, Alex H. “A Short Introduction to Optimal Transport and Wasserstein Distance.” It’s Neuronal!, October 9, 2020. https://alexhwilliams.info/itsneuronalblog/2020/10/09/optimal-transport/.
{5} OpenCV – Perspective-n-Point (PnP) pose computation, https://docs.opencv.org/4.x/d5/d1f/calib3d_solvePnP.html
One reply on “Graph-based Optimal Transport for Keypoint Matching: Extending the Sinkhorn Solver”
Nice work!