Introduction
Chladni patterns are usually created by putting some light, scattered object like sand onto a metal plate. The metal plate is then made to vibrate, which forms different patterns on the plate depending on the frequency of the wave.
Skrodzki et al. (2016) introduce a method to bring Chladni patterns into the third dimension.
Chladni patterns represent the points along which multiple waves meet to form nodes. These nodes are points along the standing wave formed by the combination of waves where a particle has 0 displacement from its mean.
Depending on the boundary condition, the final solution for the Chladni formulation varies. We can choose between Dirichlet or Neumann conditions.
\(A · sin(u · π · x) · sin(v · π · y) · sin(w · π · z) + B · sin(u · π · x) · sin(v · π · z) · sin(w · π · y) \)
\(+ C · sin(u · π · y) · sin(v · π · x) · sin(w · π · z) + D · sin(u · π · y) · sin(v · π · z) · sin(w · π · x) \)
\(+E · sin(u · π · z) · sin(v · π · x) · sin(w · π · y) + F · sin(u · π · z) · sin(v · π · y) · sin(w · π · x) \)
The above is the solution given a Dirichlet boundary condition. To get the solution with a Nuemann boundary condition, it is the same as the above solution, where all the sin functions are cos instead. More details as to the use of amplitudes and wave number are discussed by Skrodzki et al. (2016).
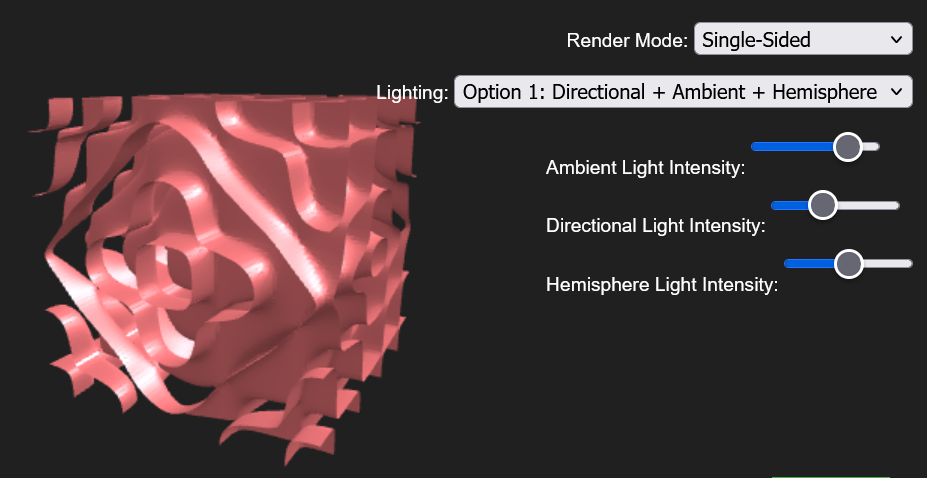
Using the solution, we can use it as an implicit surface for rendering. This can be done using a standard cube marching algorithm.
Outcome
Through the above formulation and cube marching techniques, our group created two open source web versions. A shadertoy implementation as well as a 3js implementation.
Source code and weblinks to both implementations can be seen here.
References
[1] Skrodzki, M., Reitebuch, U., & Polthier, K. (2016). Chladni Figures Revisited: A peek into the third dimension. Proceedings of Bridges 2016: Mathematics, Music, Art, Architecture, Education, Culture, 481–484. http://www.archive.bridgesmathart.org/2016/bridges2016-481.html
This blog was written by Sachin Kishan, Nicolas Pigadas and Bethlehem Tassew during the SGI 2024 Fellowship as one of the outcomes of a one week project under the mentorship of Martin Skrodzki and support of Alberto Tono as teaching assistant.