Kirby Dietz, Bonnie Magland, & Marcus Vidaurri
Introduction
What does it mean for a shape to be complex? We can imagine two shapes and decide which seems to be more complex, but is our perception based on concrete measures? The goal of this project is to develop a rigorous and comprehensive mathematical foundation for shape complexity. Our mentor Kathryn Leonard has conducted previous work on this topic, categorizing and analyzing different complexity measures. The categories include Skeleton Features, Moment Features, Coverage Features, Boundary Features, and Global Features. This week we focused primarily on two complexity measures from the Boundary Features. We tested these measures on an established database of shapes as well as producing some shapes of our own to see which aspects of complexity they measure and if they match our intuition.
Measures
Boundary
The first measure of complexity we considered was related to the boundary of the figure. To understand the measure, we first need to understand down-sampling. This is the process of lowering the number of vertices used to create the shape, and using a linear approximation to re-create the boundary. A total of five iterations were performed for each figure, typically leading to a largely convex shape.

The measure we considered was the ratio between the length of the downsampled boundary and that of the original boundary. In theory, downsampling would significantly change the boundary length of a complex shape. Thus, ratio values close to 0 are considered complex and values close to 1 are considered simple (that is, the downsampled length closely matches the original).
The boundary measure was tested on images which had been hand-edited to create a clear progression of complexity.
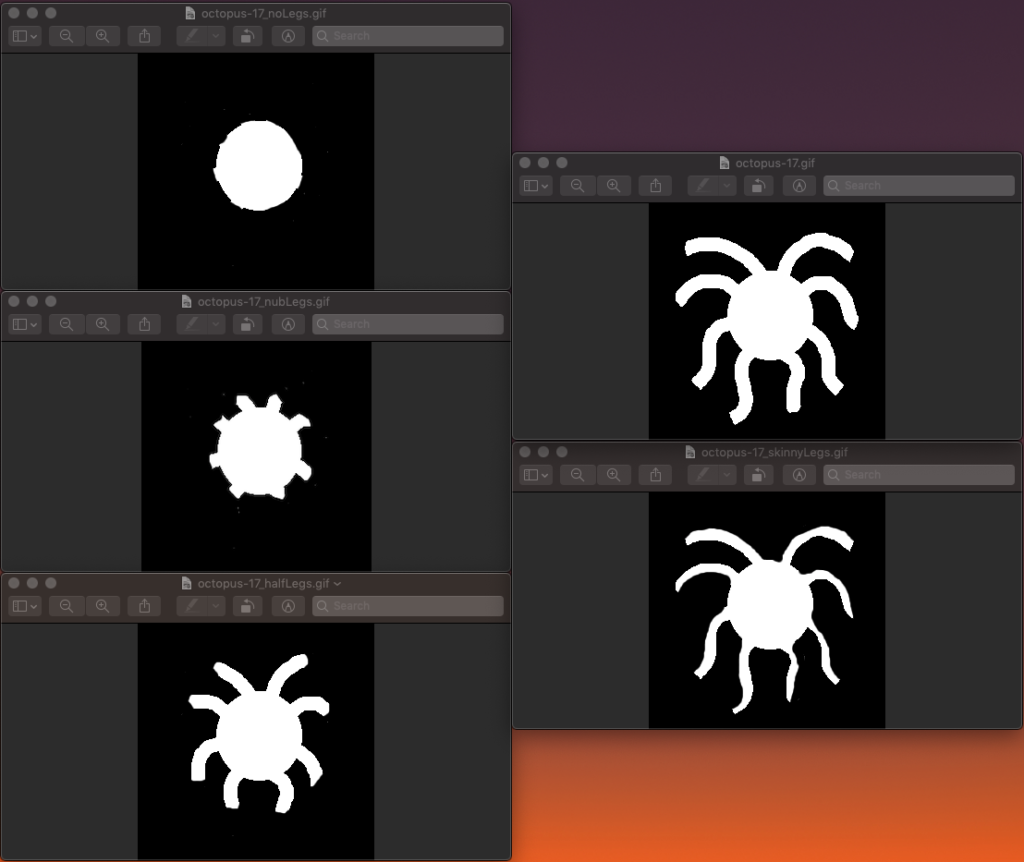
For example, the boundary measure created a ranking that nearly matched our intuition, besides switching the regular octopus and the octopus with skinny legs. For all other hand-edited progressions, the boundary measure exactly matched our intuition.
See Appendix 3 in the attached spreadsheet for the full boundary data.
Curvature
The second measure of complexity we considered was curvature. We calculate a normalized, ten bin histogram of the distribution of curvature values at each point of the shape boundary for a given shape and rank the complexity based on the value of the first bin, which was shown in user studies to be highly correlated with user rankings. Higher numbers generated from this measure indicate greater complexity.
One thing this measure emphasizes is sharp corners. At these points the curvature is very high, having a large impact on the overall value.
| 0.040800 | 0.042084 | 0.048096 |
User Ranking
To see how these measurements compared to our conception of complexity, we looked at previously created images and ranked them as a group according to our notion of complexity. One such subset of images was a group of eight unrelated figures, shown below.
We then used the two measures to create an automated ranking.
| # | Ranked by User | Ranked by Boundary Length | Boundary Length Values | Ranked by Curvature | Curvature Values |
| 1 2 3 4 5 6 7 8 | ‘lizzard-9’ ‘rat-01’ ‘ray-1’ ‘octopus-13’ ‘device1-6’ ‘Glas-9’ ‘horseshoe-9’ ‘apple-1’ | ‘octopus-13’ ‘rat-01’ ‘lizzard-9’ ‘ray-1’ ‘device1-6’ ‘Glas-9’ ‘apple-1’ ‘horseshoe-9’ | 0.67527 0.72998 0.79933 0.89246 0.93668 0.93796 0.96382 0.97621 | ‘lizzard-9’ ‘ray-1’ ‘rat-01’ ‘device1-6’ ‘octopus-13’ ‘Glas-9’ ‘apple-1’ ‘horseshoe-9’ | 0.3487 0.2004 0.2004 0.1483 0.092184 0.052104 0.044088 0.034068 |
The octopus had the lowest boundary length value, and thus the highest complexity ranking according to this measure. Much of the original figure’s perimeter is contained in the tentacles, which are smoothed out during the downsampling. This leads to a large difference in boundary lengths, meaning a more complex ranking.
As previously mentioned, the curvature measure emphasizes sharp corners. This is why the curvature measure ranks the stingray and flower higher than the boundary measure does.
To evaluate how well the resulting ranking matched with our own ordering, we used three similarity measures shown below.
| Measure | Similarity Value | Avg. Distance | Normalized Dist |
| Boundary Length | 0.3750 | 1.00 | 0.12500 |
| Curvature | 0.2500 | 0.75 | 0.09375 |
The first measure we used to compare the user and automated rankings was the ratio of the number of images with matching rank to the total number of images. We called this ratio the similarity value. For example, the user rankings and curvature rankings both placed ‘lizzard-9’ at #1 and ‘Glas-9’ at #6. Thus, the similarity value for the curvature measure was 2/8, or 0.25.
The second similarity measure we used was the average distance, the ratio of the sum of the differences in rank number for each image to the total number of images. This was included to consider how much the ranking of each image differed.
The third similarity measure was the normalized distance, the ratio of the average distance to the total number of images. This was included to account for differences in sample sizes.
The rankings of the group of eight images did differ from our ordering, but on average each shape was off by less than one rank.
Camel & Cattle
Now that we better understand each measurement, we tested them on a database of thirty-eight images of camels and cattle. As in the first example, we ranked the images in order of perceived complexity, and then generated an ordering from the boundary length and curvature measures.
| Measure | Similarity Value | Avg. Distance | Normalized Dist |
| Boundary Length | 0 | 10.31578 | 0.27146 |
| Curvature | 0.02631 | 8.68421 | 0.22853 |
This ranking was less accurate, but still had a clear similarity. We did see however similar groups of values in the boundary length, and ties within the curvature and to deal with this we ran k-mediods clustering on these bins of measures individually.
See Appendix 1 for the full data on the Camel-Cattle Rankings
K-mediods clustering is an algorithm that puts into groups or clusters pieces of data, in an attempt to minimize the distance (in this case Euclidean distance) between the points within each cluster to minimize the total of Euclidean distances summed over the distance within each cluster. For the curvature measure we got the following clusters. (Note that the boundary length and curvature measures ignore any ‘noise’ within the boundary of the image. Thus, the spots on the cows were not considered.)
This showing what the curvature measure considers the most similar shapes, and for the boundary length measure getting the following clusters:
In order to see how well the two measures did in combination, we used both quantities in a clustering algorithm to produce groupings of similar images. The resulting clusters grouped simple shapes with simple shapes, and more complex shapes with more complex shapes.
See Appendix 2 in the attached spreadsheet for the full clusters as well as their distances on the Camel-Cattle.
Polylines
To test our measures on a clear progression of complexity, we decided to make our own shapes. Using a Catmull-Rom interpolation of a set of random points (thanks day 3 of tutorial week!), we produced a large data set of smooth shapes. Generally, intuition says that the more points used in the interpolation, the more complex the resulting shape. Our measures both reflected that pattern.
| N = 5 | N = 10 | N = 15 | N = 25 |
| C: 0.022044 B: 1.0044 | C: 0.034068 B: 0.98265 | C: 0.066132 B: 0.93492 | C: 0.08016 B: 0.91145 |
See Appendix 4 in the attached spreadsheet for the full ranking data of the measures on the Polylines.
We calculated these measures on our database of over 150 shapes, each generated from five, ten, fifteen, or twenty-five points. Using these results, a clustering algorithm was able to roughly distinguish between these four groups. It groups 98.0% of the fives together, 78.7% of tens, 62.5% of fifteens, and 85.2% of twenty-fives. We also note that both complexity measures identify these shapes as much simpler than the other shapes in our database, even with the higher point orders. This is likely because of how smooth the lines are. This reveals an opportunity for future improvement in these measures, since intuition would rank a simple shape from the database (like the horseshoe) as simpler than the figure in the N = 25 column above.
See Appendix 5 in the attached spreadsheet for the clustering data of the polylines.
Noisy Circles
In order to test the measures on a clear progression of complexity that progressed the noise of the shape (small protrusions) rather than large protrusions or changes like in the Polylines we created we created a shape making program that started with a circle, something that both our intuition ad the constructive model of complexity put forth as the simplest shape. We then added noise to the circle by running a pseudo-random walk on each point on the boundary of the circle where we added a point for each step of the walk. The walk went in a random cardinal direction, a random number of steps for each point on the boundary, we then theorized that we would be able to add levels of complexity on average by increasing the number of propagations, eg: the number of times that the circle underwent every point taking a random walk. This has the additional benefit that like the polylines allows us to measure complexity on average levels which would give us a better comparison to see if our measures are reasonable.
To test this we ran eight levels of complexity with ten shapes per level. The shapes as well as what propagation, and thus complexity level each one is is shown in the first figure.
In order to give a partial test to see if our hypothesis that generally the more propagations are run the more complex the shape is we tested it against our human intuition of complexity, and ranked the shapes according to how complex they seemed to human intuition.
Comparing the two we get the following table:
| Similarity Percentage | Distance |
| 58.75% | 0.425 |
At first glance looking at the similarity percentage, that is how many of the shapes are placed by human intuition into the same complexity level as the number of perturbations, and we see that only 59% of the shapes are placed into the same level, however, looking at the distance tells us a different story. We see from the small distance value, that our similarity percentage is lower than we would like because swaps between one level and another are rather common which means that the general relation of propagations to complexity is what we desire, thus comparing distance to the original seems to be a promising measure of how accurate the propagations to complexity are. As this distance function implies that on average the complexities are in the correct level and are only moved half a level from the number of propagations done. Thus as our general hypothesis is true that the number of propagations correlates to the complexity we can look at the automatic measure of propagations rather than user intuition for comparing this data to the curvature and boundary measures.
Now that we have seen this let us look at how the curvature measure ranks the shapes. In the bottom left figure:
| Similarity Percentage | Distance |
| 0.3% | 1.2625 |
We see from the similarity, that it is less similar to the propagations, than the intuition and thus is less accurate to our intuition than the number of propagations are, however it again does not have a large distance, in fact when taking into account the distance between the the intuition and the propagation we get that the distance range between intuition and the curvature measure ranking is in the range of 0.8375-1.6875, which is not too large of a change, and shows that the curvature measure is a reasonable measure insofar that it gives us the correlation that we are looking for generally, however as we can see looking at the ranking itself in the figure it is not entirely accurate.
See Appendix 6 in the attached spreadsheet for the full ranking data for the not-circles.
We now look at the other main measure that we use the boundary length measure to see the ranking that it produces. In the bottom right figure:
| Similarity Percentage | Distance |
| 0.375% | 0.8625 |
From this data we see that in comparison to the curvature we have both a higher similarity and a lower distance. From the low distance we see that in general only small shifts between what levels things should be placed upon occur, confirmed by the difference between the boundary length measure and our intuition being in the range of 0.4375-1.2875, this shows that for looking of noise of this nature that the boundary length measure is better than the curvature measure as it keeps the general relationship and does so with much less error, thus showing a strong reason to use the boundary length measure as a way to classify the complexity of shapes differing in the amount of noise that they have.
See Appendix 6 in the attached spreadsheet for the full ranking data.
Lastly, to see whether or not these levels are somewhat arbitrary and whether there is an even gap between levels, we use k-medoids clustering on eight clusters to see how it is clustered using both the boundary length and curvature measures together. From this we get extremely interesting results, in that they say “No! There are not even gaps” we see this from the range in sizes of the clusters that occur ranging from 1 to 27, thus we see that the propagations do not create even clusters but rather bursts of complexity. This is however to be expected, the levels are simply the number of propagations that occur and we forced the earlier rankings into using the same number on each level, and thus this does not defeat that on average each level has more complexity, we also need to consider that there are some differences due to using these measures for clustering from how human intuition would cluster them. We now from seeing the lowest number of clusters have a strange result, one of the clusters has only one element in it, , and while this presents an initial puzzle after analysis it shows to have a good reason the circle like element by itself is almost a perfect (pixel) circle, thus it is placed by itself as its own level of a “zero” complexity. That many levels of propagations exist within one cluster is also similarly explained to clusters of different sizes, that is when we looked at our previous data small changes in distance were common and thus in clustering instead of small distances, where small shifts occur we instead have them in the same group.
See Appendix 7 in the attached spreadsheet for the full clusters as well as distances of the noisy circles.
Putting it all Together
Lastly we clustered everything in order to get a sense of the various complexities and how our measures would group all of the different main categories of shapes that we looked at, those being the camel-cattle, the polylines and the not circles. We put them into eight clusters in order to attempt to put them into the same category levels of complexity as were arbitrarily created by the not shape propagations. From this we got somewhat unexpected results, those being that while the camel-cattle were grouped together with the not circles, as well as with how their complexities would expect them to be grouped based on earlier clusterings, the polylines were in clusters by themselves. We then have to expand upon this clustering in order to try to explain it. The clusters of camel-cattle as well as not circles were four of the eight clusters, inside of these clusters we had on average the higher number of propagation on not circles grouped together with the camel-cattle that were given higher ranked complexity values, and vise-versa with lower propagation and lower ranked complexity. The other four clusters were the polyline data, and the reason for this is that as we can see the polylines are given by the curvature ad boundary length measures to have much less complexity and as such are in a group, well groups of their own having much less complexity than the camel-cattle as well as the not circles, and thus by our measures they are clustered separately. This is interesting especially as one of our not circles is almost just a perfect (pixel) circle, we then want to somewhat explain why this is more complex than the polylines, and the answer that we see for this is that the polylines are much smoother, while the pixel circle is still made out of these large pixels and thus is much sharper, it is thus left as a somewhat open question if this would be true for larger starting not circles.
See Appendix 8 in the attached spreadsheet for the full clusters as well as the distances of all the shapes.
Conclusion
From our tests and calculations, we conclude that our intuition of shape complexity is measurable, at least according to some respects, we saw that curvature was a good measure of how many sharp edges a shape has, and length was a measure of the noise and somewhat of the protrusions on a shape. The specific measurements of boundary length and curvature both give good estimations of complexity, giving the general relation between our intuitive understanding, while measuring in general different properties of shapes. However, we only did this research for one week and thus it feels necessary to say what would be done to continue on this research, the ways that we would continue the research is in three main facets. Firstly we would like to use more measures other than just the boundary length and curvature measures, in order to both see if there are other more effective general measures of complexity and in order for us to see if other measures are better able in particular at looking at different areas of complexity. From looking at more measures we can also increase what we consider in our k-medoids. The second thing that we would do is to compare and rank more of the shapes based on the intuition of more people, because of the subjective nature of doing this intuitive ranking. This would allow us to better with more data on subjective ranking see how accurate our complexity measurements are. On this same subject the third area we would do more research on would be to increase the number of shapes that we are looking at specifically the number of not circles, and polylines as they are randomly generated and thus only on average increase in complexity and thus with the more shapes we have of them the clearer we would see the differences in complexity between the number of points and the propagations.
Acknowledgements
We would like to express great appreciation for our mentor Kathryn Leonard, who generously devoted time and guidance during this project. We would also like to thank our TA Dena Bazazian, who provided feedback and encouragement throughout the week.