By SGI fellows Alejandro Pereira and Vivien van Veldhuizen
On the last day of the tutorial week, Nicholas Sharp gave a talk about robustness and debugging in geometry processing. He explained that there are a lot of interesting software tools available for geometry processing, but it is sometimes hard to make these tools robust to different types of data. This is especially true in geometry processing, where there are a lot of different complex data structures such as meshes. Software tools not being robust to different sorts of data, leads to a lot of the available tools becoming unusable, or results coming out wrong. It is therefore important for anyone working with geometry processing, to know what kinds of robustness problems you might encounter and how these may be solved.
Five Common Problems
Nicholas mentioned five of these common problems. The first concerned floating point numbers not being as precise as real mathematical numbers. This could lead to inaccurate data representations, which only pile up as we start computing with the less precise floating point numbers. A second problem to think about was different types of solvers. Nicholas mentioned that we often use numerical solvers in geometry processing, but that some types are a lot more fast and reliable (such as dense linear solvers) than others (for example quadratic or nonlinear solvers). Another common problem Nicholas mentioned was the problem of “bad” meshes. Preloaded meshes could for example have orientation problems, contain overlapping vertices or be nonmanifold. Moreover, even if the meshes were all structured correctly, if we want to run simulations on these meshes, a given algorithm might work on one mesh but not the other. This is because in visual computing, algorithms and inputs (in this case our meshes) are not designed together. Instead, algorithms are just a part of a pipeline and are expected to work on any input data, which is of course not always feasible in practice. Finally, Nicholas briefly talked about machine learning for geometry processing, which is often marketed as an alternative to classic geometry processing. He mentioned that actually, machine learning methods often still contain a lot of geometry processing operations under the hood, so we might still run into any of the problems mentioned above, which might also impact our machine learning results.
To show us what some these problems might look like in practice, Nick gave us two Matlab “puzzles” that we had to solve. Each of these Matlab exercises had some sort of robustness problem and our goal was to find out what these problems were and solve them.
Puzzle 1
In the first exercise, we want to plot a simple mesh. Nothing too complicated right?
Once we have a matrix of vertices V and a matrix for the faces F, it’s just a simple case of running:
>> tsurf(F, V)However, we get an error:
Error using patch
Value must be of numeric type and greater than 1.
Error in trisurf (line 95)
h = patch('faces',trids,'vertices',[x(:) y(:) z(:)],'facevertexcdata',c(:),...
Error in tsurf (line 132)
t_copy = trisurf(F,V(:,1),V(:,2),V(:,3));So, what happened? MATLAB told us the error comes from the patch function, so we call patch directly to see what is happening:
>> patches('Faces', F, 'Vertices', V)
Error using patch
Value must be of numeric type and greater than 1.Because patch only uses V and F, the problem must be in either one of those variables. What if we explicitly give it the X, Y, and Z coordinates of the vertices to plot?
>> patch('XData', V(:,1), 'YData', V(:,2), 'ZData', V(:,3), 'Facecolor', 'Blue')

Yes, progress! We plotted something, and we can see that it is a duck. The vertices matrix seems to be correct, so perhaps i is the faces F that is the problem
Remember the error in the patch function? “Value must be greater than 1.” Well, if you come from a different coding background such as Python, you know that arrays start at index=0. However, this is not the case in MATLAB, where indices start at 1. This means we just need to add 1 to F to fix the problem.
>> F= F+1
>> tsurf(F,V)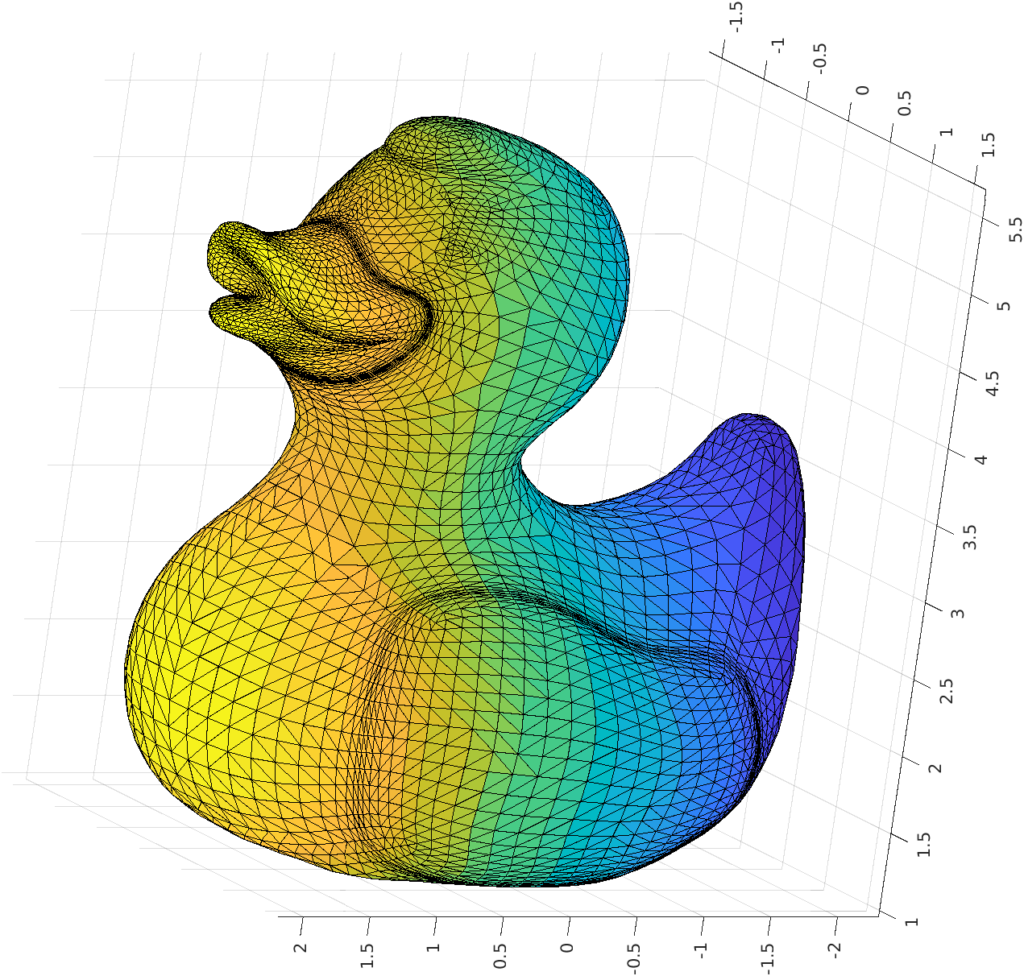
Success! We have a lovely duck. Alternatively, we could have used tsurf(F+1,V) and it would also work.
Sometimes error and warnings may be a little intimidating, but if we go step by step from the first error we can find that the source is something as simple as changing a 0 to a 1.
Puzzle 2
For the next exercise, our objective was to compute the geodesic distances along the surface of a ‘meshified’ cow.
For that we will use the 'heat_geodesic' function. In this case, running the function results in the following error:
>> dists = heat_geodesic(V,F,1);
Warning: Matrix is singular, close to singular or badly scaled.
Results may be inaccurate. RCOND = NaN.
> In min_quad_with_fixed/solve (line 409)
In min_quad_with_fixed (line 103)
In heat_geodesic (line 199)Here the problem is a little more complicated: in our quadratic solver, one of the matrices is singular. This means, among several other equivalent propositions, that the determinant of said matrix is 0.
For now, let’s try to visualize what the mesh looks like using tsurf(F,V):

At first glance, there seems to be nothing wrong. The trick is to realize that some of the vertices in the above mesh are too close to each other. This results in the matrix becoming singular.
One way to solve this is to merge vertices that are closer to a certain threshold. In this case, a threshold of 0.0001 m is enough to remove 120 vertices. The result:

Finally, we get the desired result!
In conclusion: debugging is not only important but also fun! Spending time trying to understand the problem, creating our own hypothesis of what the output should be, and then testing them is what science is all about.