By Adrish Dey, Dorothy Najjuma Kamya, and Lily Kimble
Note: Although this is an ongoing work, this report documents our progress between the official 2 weeks of the project. (August 2, 2021 – August 13, 2021)
The past 2 weeks at SGI, we have been working with David Palmer on investigating a novel Bayesian approach towards the angular synchronization problem. This blog post is written to document our work and share a sneak peek into our research.
Introduction
Consider a set of unknown absolute orientations \(\{q_1, q_2, \ldots, q_n\}\) with respect to some fixed basis. The problem of angular synchronization deals with the accurate estimation of these orientations from noisy observations of their relative offsets \(O_{i, j}\), up to a constant additive phase. We are particularly interested in estimating these “true” orientations in the presence of many outlier measurements. Our interest in this topic stems from the fact that the angular synchronization problem arises in various avenues of science, including reconstruction problems in computer vision, ranking problems, sensor network localization, structural biology, etc. In our work, we study this problem from a Bayesian perspective, by modelling the observed data as a mixture between noisy observations and outliers. We also investigate the problem of continuous label switching, a global ambiguity that arises from the lack of knowledge about the basis of the absolute orientations \(q_i\). Finally, we experiment on a novel Riemannian gradient descent method for alleviating this continuous label switching problem and provide our observations herein.
Brief Primer on Bayesian Inference
Before going deeper, we’ll briefly discuss Bayesian inference. At the heart of Bayesian inference lies the celebrated Bayes’ rule (read \(a|b\) as “a given b”):
\[\underbrace{P(q | O)}_{\textrm{posterior}} = \frac{\overbrace{P(O|q)}^{\textrm{likelihood}} \cdot \overbrace{P(q)}^{\textrm{prior}}}{\underbrace{\int\limits_q P(O|q)\cdot P(q)}}_{\textrm{evidence}}\]
In our problem, \(q\) and \(O\) denote the true orientations that we are estimating and the noisy observations with outliers respectively. We are interested in finding the posterior distribution (or at least samples from it) over the ground truth \(q\) given the noisy observations \(O\).
The denominator (i.e., the evidence or partition function) is an integral over all \(q\)s. Exactly evaluating this integral is often intractable if \(q\) lies on some continuous manifold, as in our problem. This makes drawing samples from the posterior becomes hard.
One way to avoid computing the partition function is a sampling method called Markov Chain Monte Carlo (MCMC). Intuitively, the posterior is approximated by a markov chain whose transitions can be computed using a simpler distribution called the proposal distribution. Successive samples are then accepted or rejected based on an acceptance probability designed to ensure convergence to the posterior distribution in the limit of infinite samples. Simply put, after enough samples are drawn using MCMC, they will look like the samples from the posterior\(P(q|O) \propto P(O|q) \cdot P(q)\) without requiring us to calculate the intractable normalization \(P(O) = \int\limits_q P(O|q)\cdot P(q)\). In our work, we use Hamiltonian Monte Carlo (HMC), an efficient variant of MCMC, which uses Hamiltonian Dynamics to propose the next sample. From an implementation perspective, we use the built-in HMC sampler in Stan for drawing samples.
Mixture Model
As mentioned before, we model the noisy observation as a mixture model of true distribution and outliers. This is denoted by (Equation 1):
\[
O_{i, j} = \begin{cases}
q_i q_j^T + \eta_{i, j} & \textrm{with prob. } p \\
\textrm{Uniform}(\textrm{SO}(D)) & \textrm{with prob. } 1 – p
\end{cases}
\]
where \(\eta_{i j}\) is the additive noise to our true observation, \(q_i q_j^T\) is the relative orientation between the \(i^\textrm{th}\) and \(j^\textrm{th}\) objects, and \(\textrm{Uniform}(\textrm{SO}(D))\) is the uniform distribution over the rotation group \(\textrm{SO}(D)\), representing our outlier distribution. \(\textrm{SO}(D)\) is the space where every element represents a D-dimensional rotation. This mixture model serves as the likelihood \(P(O|q)\) for our Bayesian framework.
Sampled Result
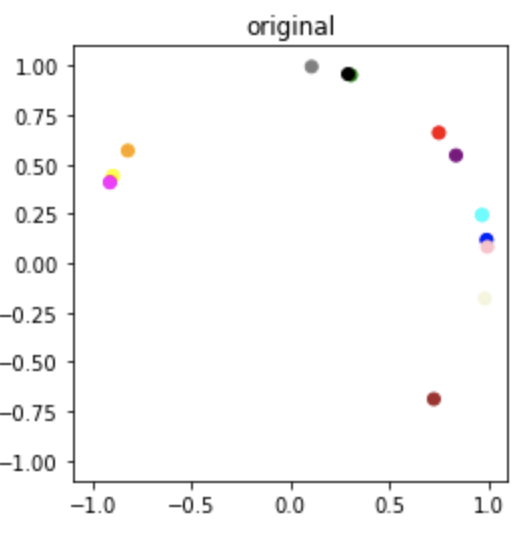
Ground truth samples of \(q_i\) 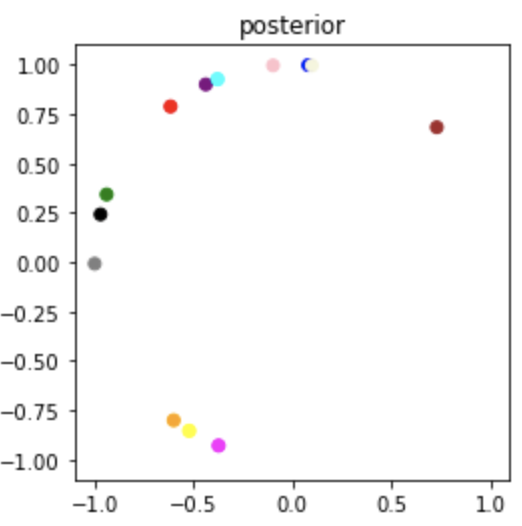
\(\hat{q}_i \sim p(q|O)\) (estimated \(q_i\)) sampled from our posterior \(p(q|O)\)
The orientations \(\hat{q}_i\) sampled from the posterior look significantly rotated with respect to the original samples. Notice this is a global rotation since all the samples are rotated equally. This problem of global ambiguity of absolute orientations \(q_i\) arises from the fact that the relative orientations \(q_i q_j^T\) and \(\tilde{q}_i \tilde{q_j}^T\) of two different set of vectors can be the same even if the absolute orientations are different. The following section goes over this and provides a sneak peek into our solution for alleviating this problem.
Continuous Label Switching
A careful observation of our problem formulation (Equation 1) would reveal the problem is invariant to transformation of the absolute orientations as long as the relative orientations are preserved. Consider the 2 pairs of observations in the figure below. (Blue and Red; Yellow and Green) Let the absolute orientations be \(q_1\), \(q_2\), \(\tilde{q}_1\) and \(\tilde{q}_2\) and relative orientations between the pairs be \(R_{12}\) and \(\tilde{R}_{12}\). As the absolute orientations \(q_1\) and \(q_2\) are equally rotated by a rotation matrix \(A\), the relative orientation between them \(R_{12}\) is preserved.
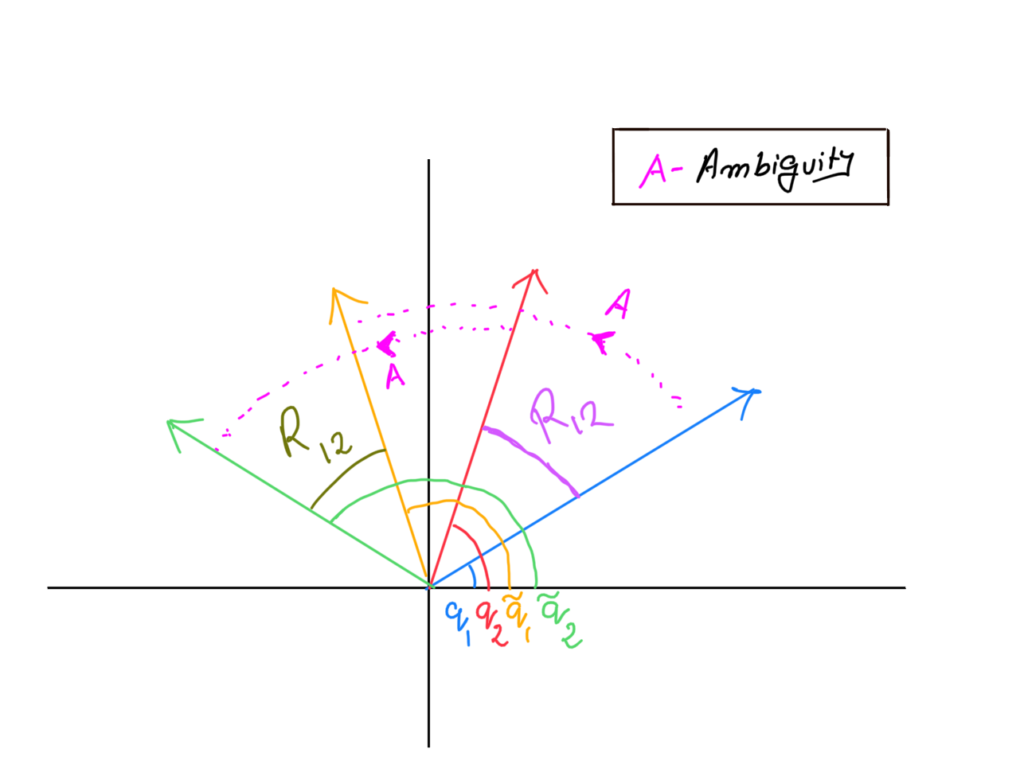
More formally, Let \(A \in \textrm{SO}(D)\) be a random orientation matrix in D-dimensions. The following equation demonstrates how rotating two absolute orientations \(q_i\) and \(q_j\) by a rotation matrix \(A\) preserves the relative orientations — which in turn gives rise to a global ambiguity in our framework.
\[
R_{ij} = q_i q_j = q_i A A^T q_j = (q_i A) (A^T q_j) = \tilde{q_i} \tilde{q_j}
\]
Since our inputs to the model are relative orientations, this ambiguity (known as label switching) causes our Bayesian estimates to come randomly rotated by some rotation \(A\).
Proposed Solution
Based on Monteiller et al., in this project we explored a novel solution for alleviating this problem. The intuition is that we believe the unknown ground truth is close to the posterior samples up to a global rotation. Hence we try to approximate the ground truth by starting out with a random guess and optimizing for the alignment map between the estimate and the ground truth. Using this alignment map, and the posterior samples, we iteratively update the guess, using a custom Riemannian Stochastic Gradient Descent over \(\textrm{SO}(D)\).
Algorithm
- Start with a random guess \(\mu \sim \mathrm{Uniform}(\mathrm{SO}(D))\).
- Sample \(\hat{q} \sim P(q | O)\), where \(P(q | O)\) is the posterior.
- Find the global ambiguity \(R\), between \(\hat{q}\) and \(\mu\). This can be obtained by solving for \(\mathrm{argmin}_R \, \| \mu – R \hat{q}\|_\mathrm{F}\).
- Move \(\mu\) along the shortest geodesic toward \(\hat{q}\).
- Repeat Steps 2 – 4 until convergence. Convergence is detected by a threshold on geodesic distance.
Results
We use this method to estimate the mean of the posterior over \(\mathrm{SO}(2)\) and plot the results (i.e. 2D orientations) in the complex plane as shown below.
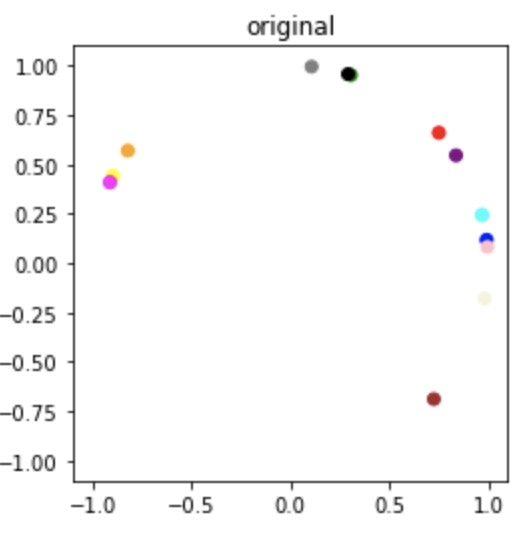
Original Sample 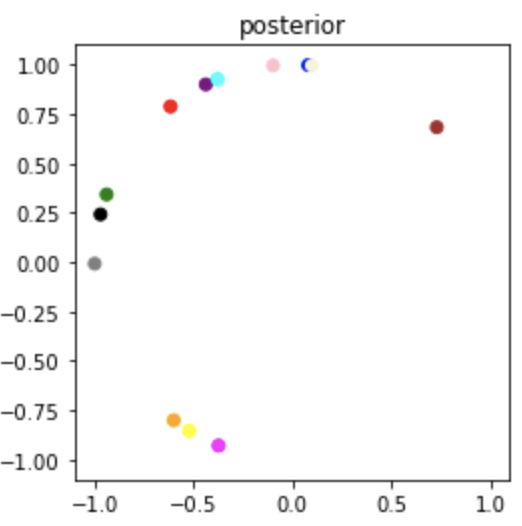
Sampled Posterior 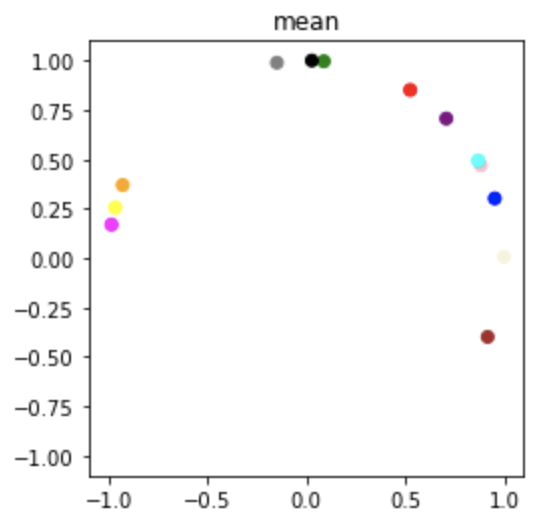
Optimized Mean Posterior
Conclusion
In conclusion, we study the rotation synchronisation problem from a Bayesian perspective. We explore a custom Riemannian Gradient Descent procedure and perform experiments in the \(\mathrm{SO}(2)\) case. The current method is tested on a simple toy dataset. As future work we are interested in improving our Bayesian model and benchmarking it against the current state-of-the-art. There are certain performance bottlenecks in our current architecture, which constrain us to test only on \(\mathrm{SO}(2)\). In the future, we are also interested in carrying out experiments more thoroughly in various dimensions. While the current MCMC procedure we are using does not account for the non-Euclidean geometry of the space of orientations, \(\mathrm{SO}(D)\), we are looking into replacing it with Riemannian versions of MCMC.