As the whirlpool of the first week of SGI came to an end, I felt that I’d learnt so much and perhaps not enough at the same time. I couldn’t help but wonder: Did I know enough about geometry processing (…or was it just the Laplacian) to actually start doing research the very next week? Nevertheless, I tried to overcome the imposter syndrome and signed up to do a research project.
I joined Professor Marcel Campen’s project on “Improved 2-D Higher Order Meshing” for Week 2. The project focused particularly on higher order triangle meshes, which are characterized by their curved (rather than straight) edges. We studied a previously presented algorithm for the generation of these meshes in 2D, with the goal of improving or generalizing it.
After an initial trial, where we struggled to get the program running on our systems, we discussed potential areas of research with Professor Campen and dived straight into the implementation of our ideas. The part of the algorithm that I worked on was concerned with the process of splitting given Bézier curves (for the purpose of creating a mesh), particularly how to choose the point of bisection, \(t\). During a later stage of the algorithm, the curves are enveloped by quadrilaterals (or two triangles with a curved edge). If two quads intersect, we must split one of the curves. The key idea here was that the quads could then potentially inform how the curves were to be split. Without going into too much technical detail, I essentially tried to implement different approaches to optimize the splitting process. The graph below shows a snippet of my results.
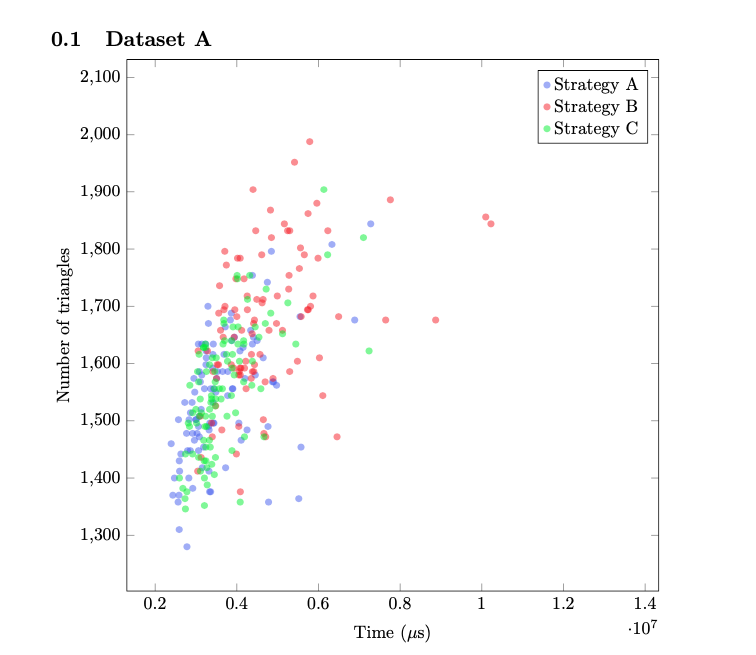
While Strategy A is the original algorithm implementation, Strategy B and C were possible improvements to it. For both of the latter strategies I used an area function to find the point where the resulting quads would have the approximately equal area. This equal distribution could point to an optimal solution. The difference between B and C has to do with how the value of \(t\) is iteratively changed as is shown below.

While I was only able to run the program on a sample size of 100 2D images, basic quantitative analysis pointed towards Strategy A and C as the more optimal choices. However, to get more conclusive results, the strategies need to be tested on more data. In addition to Strategy B and C, another direction for further consideration was to use the corners of the quad to find the projection of the closest corner to the curve.
As the week came to an end, I was sad to leave the project at this somewhat incomplete stage. During the week, I went from nervously reading my first research paper to testing potential improvements to it. It was an exciting week for me and I can’t wait to see what’s next!