Authors: Bryce Van Ross, Deniz Ozbay, Talant Talipov
The following is a summary of three Week 5 talks, presented on behalf of students in the MIT Summer Geometry Institute. These summaries were made by members of the team of the Hausdorff Distance group. Topics include: Partitioned Solid-Fluid Coupling, Graduate School Panel and Q&A, and Developments in Smooth Optimization Contact.
Partitioned Solid-Fluid Coupling
This talk was presented by Dr. Tamar Shinar at University of California, Riverside. I liked this talk for several reasons. From an introductory physics background, we are aware that forces act on multiple objects. Depending on the type of object, certain forces behave differently with respect to the object and we use certain equations to model this interaction. However, as the system of objects becomes mixed, our use of forces becomes more complex. So, the modeling efforts must adapt accordingly. This lecture focused on how to model fluid-structure interaction (FSI), commonly referred to as solid-fluid coupling, via numerical algorithms, and discussed related applications. Examples of applications typically include fluid dynamics or animation. As suggested by Dr. Shinar, more intuitive, concrete examples are modeling the flight of a bird in the air (Figure 1), or the movement of a straight hair flip relative to a medium of water (Figure 2).
Solid-fluid coupling models the dynamics of fluids and solids. Specifically, these dynamics are computed simultaneously, which can be problematic. The challenge in this field is to make it less so, while ensuring a reflective representation of the physical forces at work. In 1- way coupling, the solid (or fluid) affects the fluid (solid), but not vice versa. This is not the case for 2-way coupling, where both objects affect each other, imposing more constraints upon the system. To account for each object’s phenomena, there exists solid and fluid handlers to model these phenomena, respectively. These solvers utilize a variety of boundary conditions, familiar to us from past math/physics courses, such as the Dirichlet, Navier-Stokes, and Neumann equations. Depending on the object and conditions, desirable properties are optimized. For solids, these would be mass and acceleration, whereas for fluids, these are position and velocity. The solution lies in the mixed-solver, and which numerical methods best model these behaviors.
There are multiple options to go about optimizing coupled-interaction. Partitioning the solver is a popular approach. In this approach, fixed point iteration and Newton’s method are strategies that solve the nonlinear system of equations, linearizing the 2-way coupling in terms of the solid and fluid. The partitioned methods tend to be more modular and easier to implement. In contrast, monolithic methods are more stable, have better performance, and handle closed regions better. In comparison to each other, their strengths are the other’s weaknesses. Common risks are that iterations can be computationally expensive and/or that they won’t converge at all. This is remedied by incorporating a reduced model interface (RMI), which serves as an intermediary lightweight solver between the solid and fluid. In effect, the RMI helps estimate tricky Jacobians in a least-weight sense. Dr. Shinar’s research specifically compares these numerical schemes in reference to an under-relaxation variable, which optimizes solution oscillations and aids in stability. The smaller this value, the slower and less efficient the computational time, in tradeoff for increased stability. The takeaways here are that the partition approach in isolation fails in terms of convergence, and the Partition-Coupling and RMI under low under-relaxation will yield optimal convergence in the shortest time. There still remain certain bounded regions, like (incompressible) Dirichlet regions, which interfere with the dynamics of known solid-fluid coupling techniques, but this has yet to be explored. For more information regarding Dr. Shinar’s research, please refer here.
An extended partitioned method for conservative solid-fluid coupling (Video from YouTube)
Developments in Smooth Optimization Contact
Professor Chenfanfu Jiang’s talk on “Developments in Smooth Optimization Contact” was really interesting for many reasons. Essentially the problem they were trying to solve was “How to model contact as a smooth problem”. This helps us accurately simulate solids which allows us to create realistic animations and benefits industry fields that use these simulations. For example in the fashion industry, these simulations provide feedback to the design of the garment.
Firstly, Dr. Jiang presented different ways to approach the problem and the advantages and shortcomings of these approaches. Then, he gave a formulation of how they came up with a solution using these, which was really interesting as it combined various approaches to come up with a better working algorithm. The research problem was also simple to understand but the tools used to solve the problem were very advanced, which was also very intriguing.
To solve this problem three main tools were used: nonlinear optimization based integrator which simulated large deformation with large steps, variational frictional contact and its extension to higher dimensions. To start with, the solution is an optimization based time integrator for electrodynamics. It is based on incremented time steps, which creates an entirely new problem at each time step. The ODE consists of an inertia term and elasticity term – which makes the problem harder as the elasticity term can be highly nonlinear and non convex. This simulates deformations based on squashing and stretching. For a more physically accurate solution, contact is added as a constraint. This constraint in the form of an inequality, makes the differential equation even harder to solve. To overcome this challenge, different approaches were developed based on previous ways to solve the problem.
The difficulty arises from the fact that the formulated constraints and ODEs that are non-smooth and non-linear, for example, when the distance between objects is zero, we have a non-smooth constraint. To overcome this, the problem is turned into a smooth and unconstrained problem by using the incremental potential contact method which guarantees intersection and parameter tuning free simulations which are stable and accurate, and the barrier method, which turns the problem into an unconstrained problem where Newton iteration can be applied.
Dr. Jiang also discussed some methods that can improve their algorithm such as clamping the barrier function, and the shortcomings such as the difficulty of implementing friction in the optimization problem. Again, the challenges arise from the function becoming non-smooth, which he mentioned can be solved by approximately defining the variational friction as a smooth function.
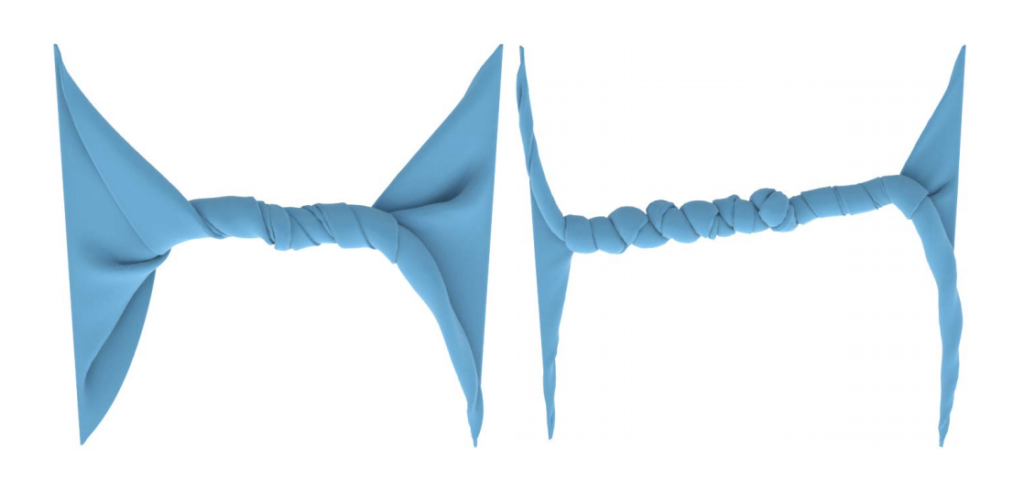
The most intriguing part of the talk was how they were able to build on existing approaches to turn the problem into a smooth one. Although the techniques they used were very advanced, the idea behind the solution was simple to understand. The simulations (especially the twisting of the cloth) Dr. Jiang showed were also really interesting; it was fascinating to see the difference between two simulations of the same object and how they become visibly more accurate as the constraints change.

Graduate School Panel
Last week I attended a talk about applications to PhD programs that was organized by Leticia Mattos Da Silva, Silvia Sellán, Jiayi Eris Zhang and Oded Stein.
One of the most exciting deals for every student is application for graduate programs. Most students are always confused with this procedure: they do not know what to write in a motivation letter and how to contact the prospective referee. All these questions were answered in this lecture. This lecture was filled with a lot of useful information about all the steps of applications to universities: from motivation letters to the choice of prospective scientific advisor. It was really interesting on the grounds that the lecturers experienced this procedure firsthand. Moreover, the speakers showed their own essays as successful examples.
As I know from this talk, the motivation letter has a specific structure. The applicant has to mention his previous research experience, why he wants to study exactly on this program, and why the university has to choose this person among the others. Furthermore, there should not be any information that is not relevant to the program: if you are applying to a PhD program in Mathematics, then you do not have to say about your background in knitting. The best moments were when the lecturer highlighted the most frequent mistakes of applicants and I realized that I did it in my motivation letter.
The recommendation letters are one of the most significant parts of the application. That is why the applicant should connect with his referee in advance. The best choice would be the person who did some research with you. In addition, you should have more referees in the case that the main ones reject.
It was a very valuable experience to listen to this lecture!