Many of the SGI fellows experienced an error using the png2poly function from the gptoolbox: when applied to the example picture, the function throws an indexing error and in some cases makes Matlab crash. So, I decided to investigate the code.
The function png2poly transforms a png image into closed polylines (polygons) and applies a Laplacian smoothing operation. I found out that this operation was returning degenerated polygons, which later in the code was crashing Matlab.
But first, how does Laplacian smoothing work?
I had never seen how a smoothing operation works, and I was surprised with how simple the idea of Laplacian smoothing is. It’s an iterative operation, and at each iteration the positions of the vertices are updated using local information, the position of neighbor vertices.

\[p_i \gets p_i + \frac{(p_{i+1} – p_i)}{2} + \frac{(p_{i-1} – p_i)}{2}\]
In polylines, every vertex has 2 neighbors, apart from boundary vertices, to which the operation is not applied. For closed polylines, Laplacian smoothing converges to a single point after many iterations.
The Laplacian matrix \(L\) can be used to apply the smoothing for the whole polyline at once, and a Lambda parameter (0 ≤ λ ≤ 1) can be introduced to control how much the vertices are going to move in one iteration:
\[p \gets p + \lambda L p\]
The best thing about Laplacian smoothing is that the same idea pleasantly applies for meshes in 3D! The difference is that in meshes every vertex has a variable number of neighbors, but the same formula using the Laplacian matrix can be used to implement it.
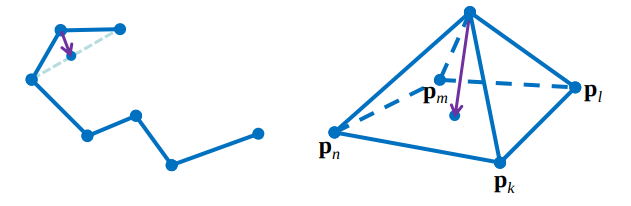
For more details on smoothing, check out this slide from Stanford, from which the images in this post were taken. It also talks about ways to improve this technique using an average of the neighbors weighted by curvature.
What about the bug?
The bug was the following: For some reason, the function that converts the png into polygons was generating duplicate vertices. Later in the code, a triangulate function is used on these polygons, and the duplicate vertices by themselves make the function crash. But even worse, when smoothing is applied to a polygon with duplicate vertices, strange things happen. Here’s an example of a square with 5 vertices (1 duplicated); after 3 iterations it becomes a non-simple polygon:
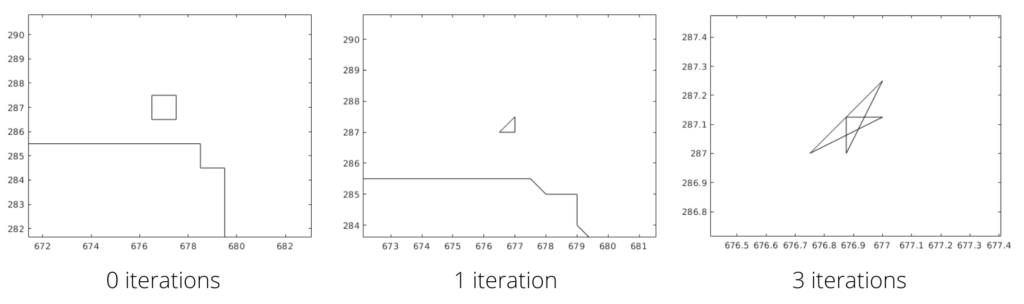
You can try to simulate the algorithm to see that it happens.
Also, the lambda parameter used was 1.0, which was too high, making small polygons collapse or generating new duplicate points, so I proposed 0.5 as the new parameter. For closed curves, Laplacian smoothing will converge to a single point, making the polygon really small after many iterations, which is also a problem for the triangulation function. In most settings, these converged polygons can be erased.
Some other problems were also found, but less relevant to be discussed here. A pull request was merged into the gptoolbox repository removing duplicate points and fixing the other bugs, and now the example used in the tutorial week should work just fine. The changes I made don’t guarantee that the smoothing operation is not generating self-intersection anymore, but for most cases it does.
Fun fact: There’s a technique for finding if a polygon has self-intersection called sweep line, which works in \(O(n\log n)\)—more efficient than checking every pair of edges!
The things I learned
- Laplacian smoothing is awesome.
- It’s really hard to build software for geometry processing that works properly for all kinds of input. You need to have complete control over degenerate cases, corner cases, precision errors, … the list goes on. It gets even harder when you want to implement something that depends on other implementations, that may by themselves break with certain inputs. Now I recognize even more the effort of professor Alec Jacobson and collaborators for creating gptoolbox and making it accessible.
Big thanks to Lucas Valença, for encouraging me to try and solve the bug, and to Dimitry Kachkovski, for testing my code.