This week I worked on the “Robust computation of the Hausdorff distance between triangle meshes” project with our mentor Dr. Leonardo Sacht, TA Erik Amezquita and my team Talant Talipov and Bryce Van Ross.
We started our project by doing some initial reading about the topic. Hausdorff distance from triangle meshes A to B is defined as $$h(A,B) = \max_{p \in A}d(p,B)$$ where d is the Euclidean norm. Finding the Hausdorff distance between two triangle meshes is one way of comparing these meshes. We note that the Hausdorff distance from A to B might be different from the Hausdorff distance from B to A, as you can see in the figure below, so it is important to distinguish which one is being computed.
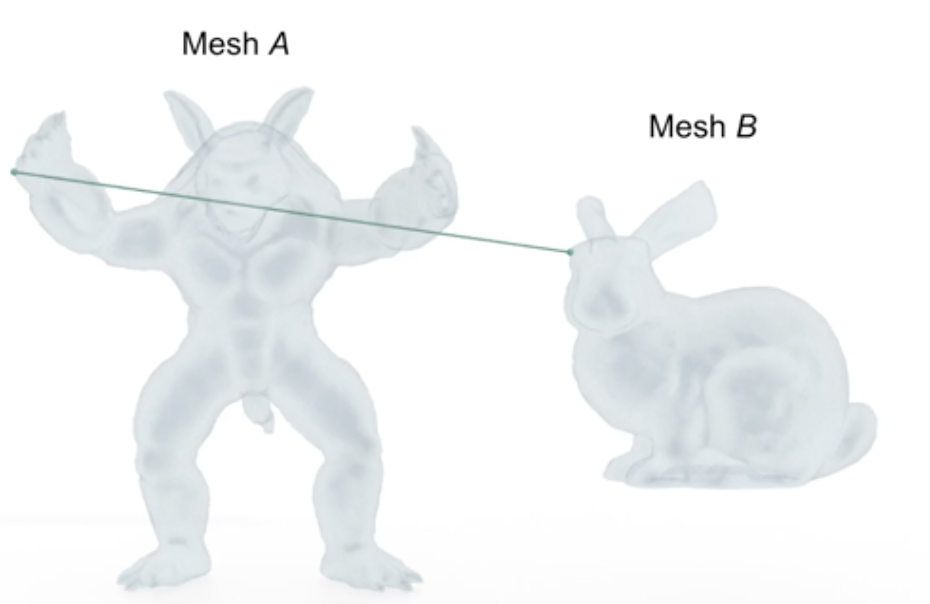
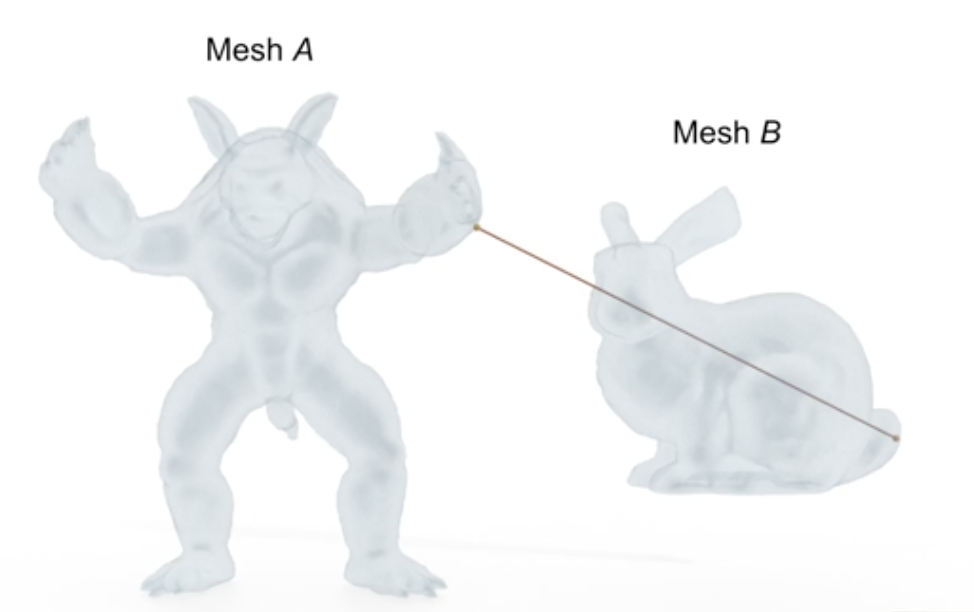
Finally we define $$H(a,b) = \max{h(A,B), h(B,A)}$$ and use this value that is symmetric when comparing triangle meshes A and B.
Our first task was to implement Branch and Bound methods for calculating this distance. Suppose we want to calculate the Hausdorff distance from mesh A to mesh B. There were three main steps in the algorithm to do this: calculation of the upper and lower bound for the Hausdorff distance, and discarding and subdividing triangles according to the values of the upper and lower bound.
The upper bound for each triangle in A is calculated by taking the maximum of the distances from the given triangle to every vertex in B. The lower bound is calculated over A by taking the minimum of the distances from each vertex p in A to the triangle in B that is closest to p. If a triangle in A has an upper bound that is less than the lower bound, the triangle is discarded. After the discarding process, the remaining triangles are subdivided into four triangles and the process is repeated with recalculation of the upper bounds and the lower bound. The algorithm is run until the values for the upper and lower bound are within some ε of each other. Ultimately, we get a triangle region that contains the point that realizes the Hausdorff distance from A to B.
To implement this method, my teammates tackled the upper and lower bound codes while I wrote an algorithm for the discarding and subdividing process:
We ran this algorithm with testing values u = [1;2;3;4;5] and l = 3 and got these results:


As expected, the two triangles that had the upper bound of 1 and 2 were discarded and the rest were subdivided.
The lower bound algorithm turned out to be more challenging than we anticipated, and we worked together to come up with a robust method. Currently, we are working on finishing up this part of the code, so that we can run and test the whole algorithm. After this, we are looking forward to extending this project in different directions, whether it is a more theoretical analysis of the topic or working on improving our algorithm!
One reply on “Branch-and-bound method for calculating Hausdorff distance”
[…] The faces are subdivided in the following way: we add the midpoints and triangles that are generated by the previous vertices and these new points. In the end, we have 4 new faces instead of the old one. For more theoretical details you should check this blog post: http://summergeometry.org/sgi2021/branch-and-bound-method-for-calculating-hausdorff-distance/ […]