Isogeometric analysis (IGA) is an analysis technique that combines computer aided design (CAD) with traditional finite element analysis (FEA). It uses the same spline basis functions to construct the geometry and the solution space, which is beneficial as traditional FEA requires geometric approximation that can lead to inaccuracies [1].
For our week 3 project, my group and I used IGA simulation software that has been developed for modelling material transport in neurons. The software solves Navier-Stokes equations to obtain the velocity field and models the transport process by reaction-diffusion-transport equations. For our purposes, we used the solver to simulate material transport in complex neurons and heat transfer processes in various geometries including a simple block model and a rod model [2].
Our project was split into two main parts: geometric modeling and analysis. For geometric modelling, we used two open source software packages (HexGen and Hex2Spline [3]) for the construction of geometries, and we then used the aforementioned IGA software for simulation purposes. I was in charge of using the IGA software to run the simulations and visualizing the results with Paraview (a visualization application).
In this post, I’ll demonstrate our results using the simple model the team created and also share some of the results I got using the IGA software on some additional models.
Here is the example model we used:
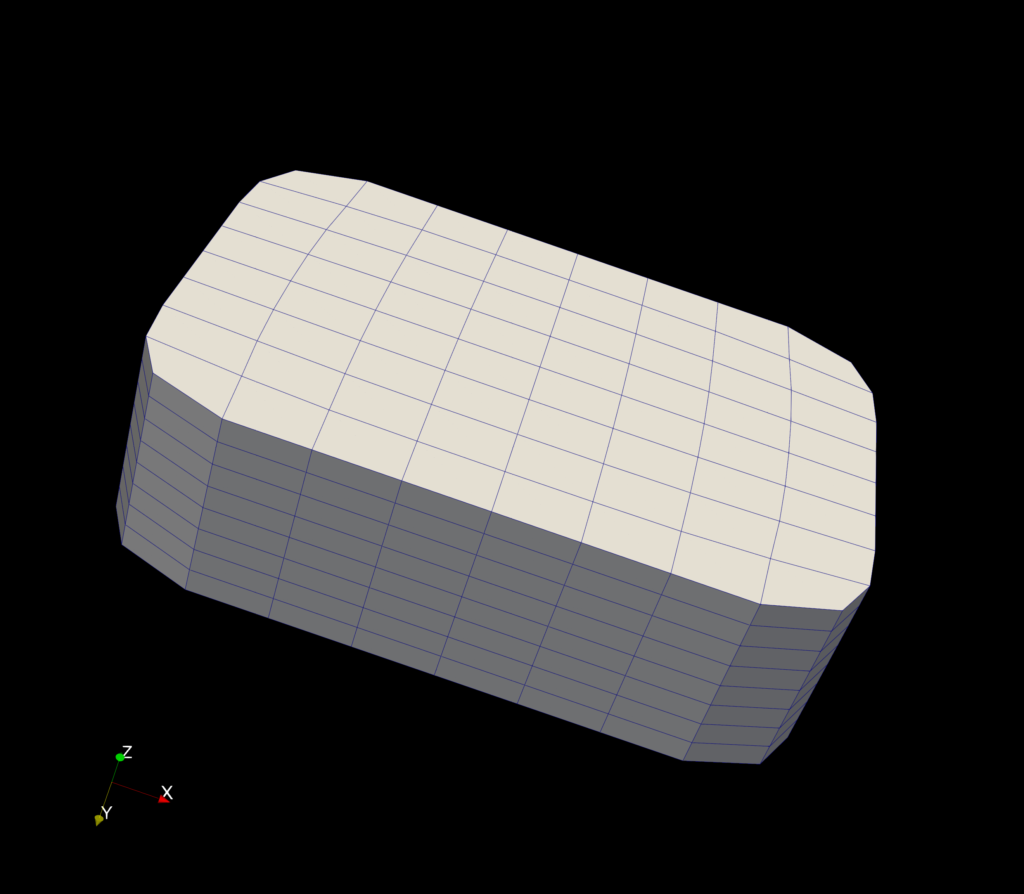
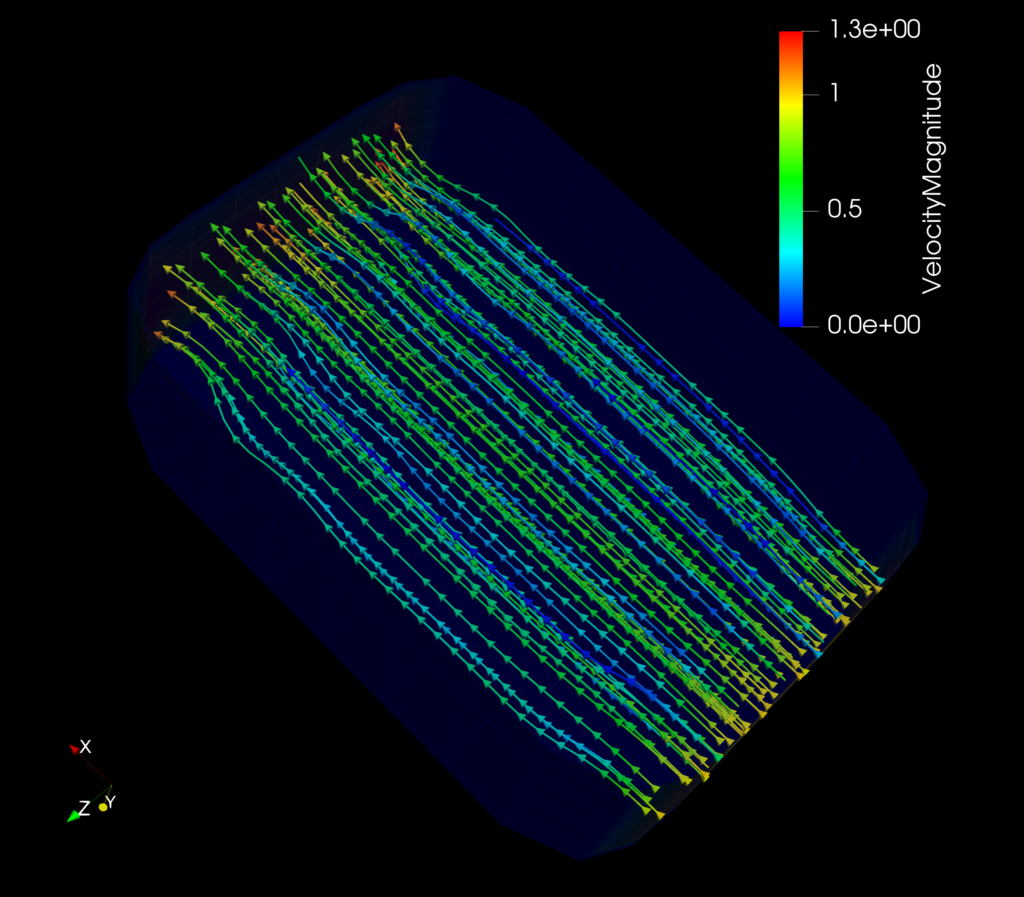
After the geometric modeling stage, I received 3 input files that contained the control mesh, an initial velocity field and the simulation parameters (particle concentrations, diffusion coefficient, velocities of material, etc.). These files were used as input for the IGA solver [2], which consists of four stages: spline construction, mesh partition for parallel computing, solving Navier-Stokes equations, and final transport simulation.
Due to the high computational needs of the last two stages, we set up the simulation environment at the Pittsburgh Supercomputer Center (PSC). We ran the simulation by connecting to the remote supercomputer via an ssh client. Finally, after getting the results, I was able to visualize them using Paraview.
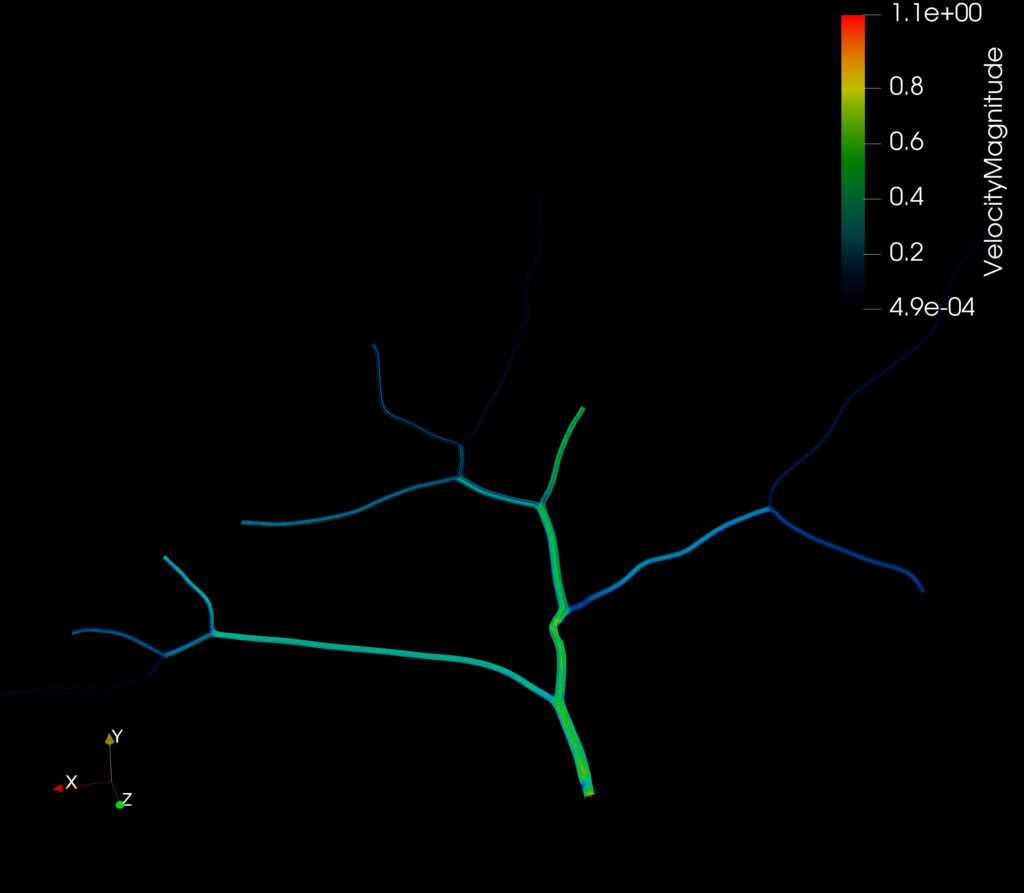
In the above example, the color bar shows the transport velocity magnitude. I also added streamlines that show the direction of flow.
Here is an animation of our results that depicts the movement of the particles:
I also ran the solver on a rod model (that Angran Li, our mentor, provided):
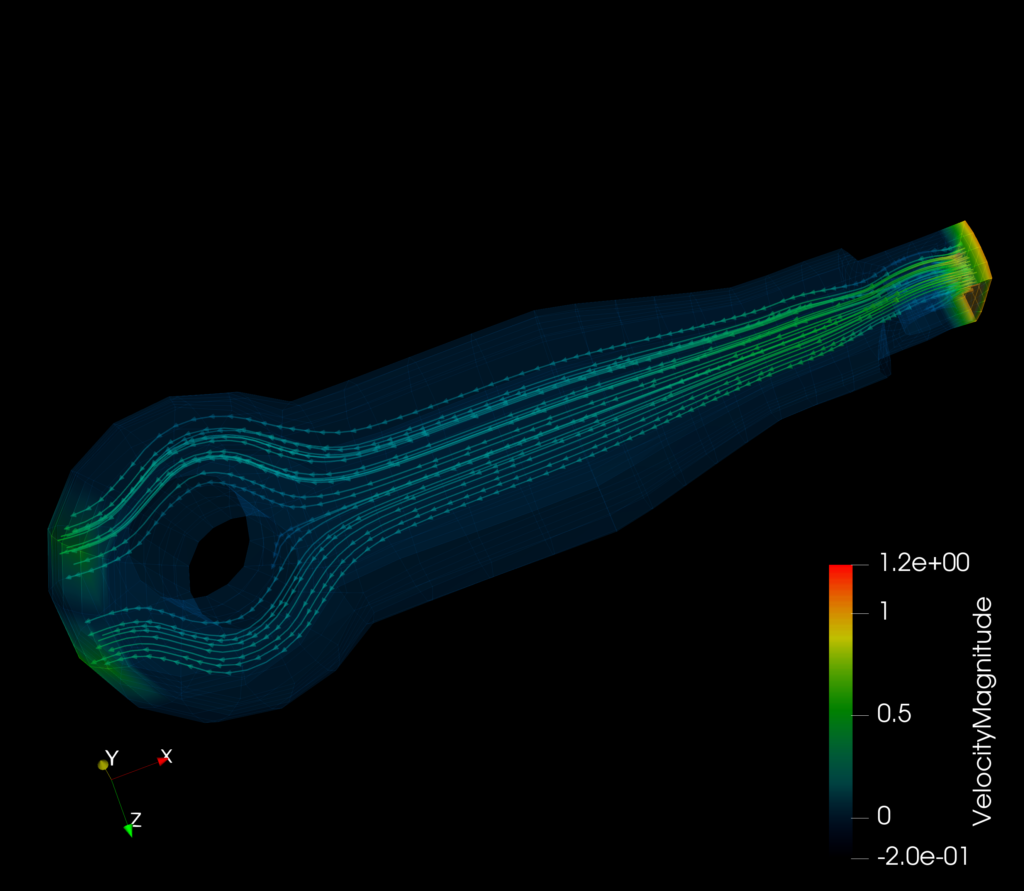
The model shows the flow of heat through the rod as it is input from the right end of the model. Again, the colorbar represents the magnitude of the velocity of particles at that point.
Finally, I also ran the IGA solver on a neuron model (found on NeuroMorpho.org and edited with the help of Angran).
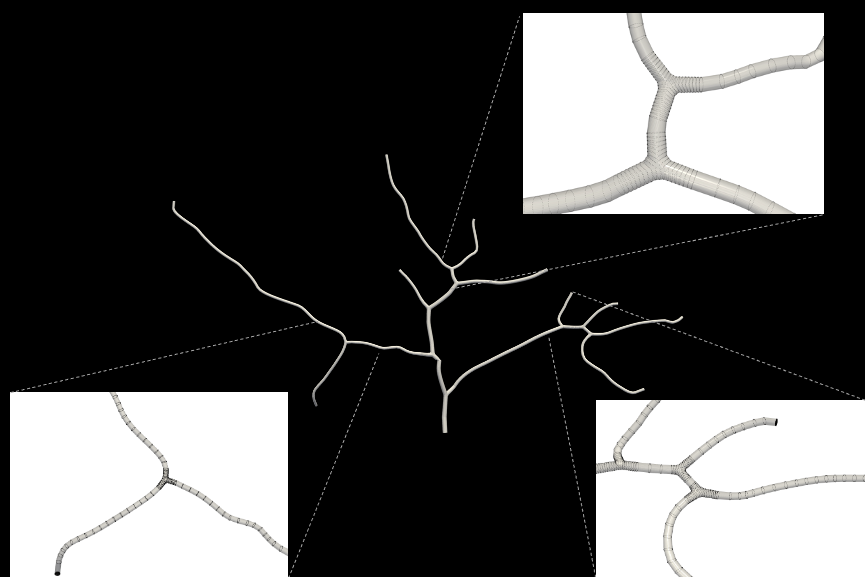
From using the remote computer to editing the neurons for our analysis, I learned a ton of new techniques during the week. I enjoyed learning about the IGA solver and its applications ranging from neuroscience to engineering. I’d like to end this post by thanking Angran his support and for bearing with me through my 1000 questions—it was a pleasure learning with you! 🙂
References:
[1] T. J. Hughes, J. A. Cottrell, Y. Bazilevs. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39-41), 4135-4195, 2005.
[2] A. Li, X. Chai, G. Yang, Y. J. Zhang. An Isogeometric Analysis Computational Platform for Material Transport Simulations in Complex Neurite Networks. Molecular & Cellular Biomechanics, 16(2):123-140, 2019. GitHub link: https://github.com/CMU-CBML/NeuronTransportIGA
[3] Y. Yu, X. Wei, A. Li, J. G. Liu, J. He, Y. J. Zhang. HexGen and Hex2Spline: Polycube-Based Hexahedral Mesh Generation and Unstructured Spline Construction for Isogeometric Analysis Framework in LS-DYNA. Springer INdAM Serie: Proceedings of INdAM Workshop “Geometric Challenges in Isogeometric Analysis”. Rome, Italy. Jan 27-31, 2020. GitHub link: https://github.com/CMU-CBML/HexGen_Hex2Spline