Fellows: Munshi Sanowar Raihan, Daniel Perazzo, Francheska Kovacevic, Gabriele Dominici
Volunteer: Elshadai Tegegn
Mentors: Silvia Sellán, Dena Bazazian
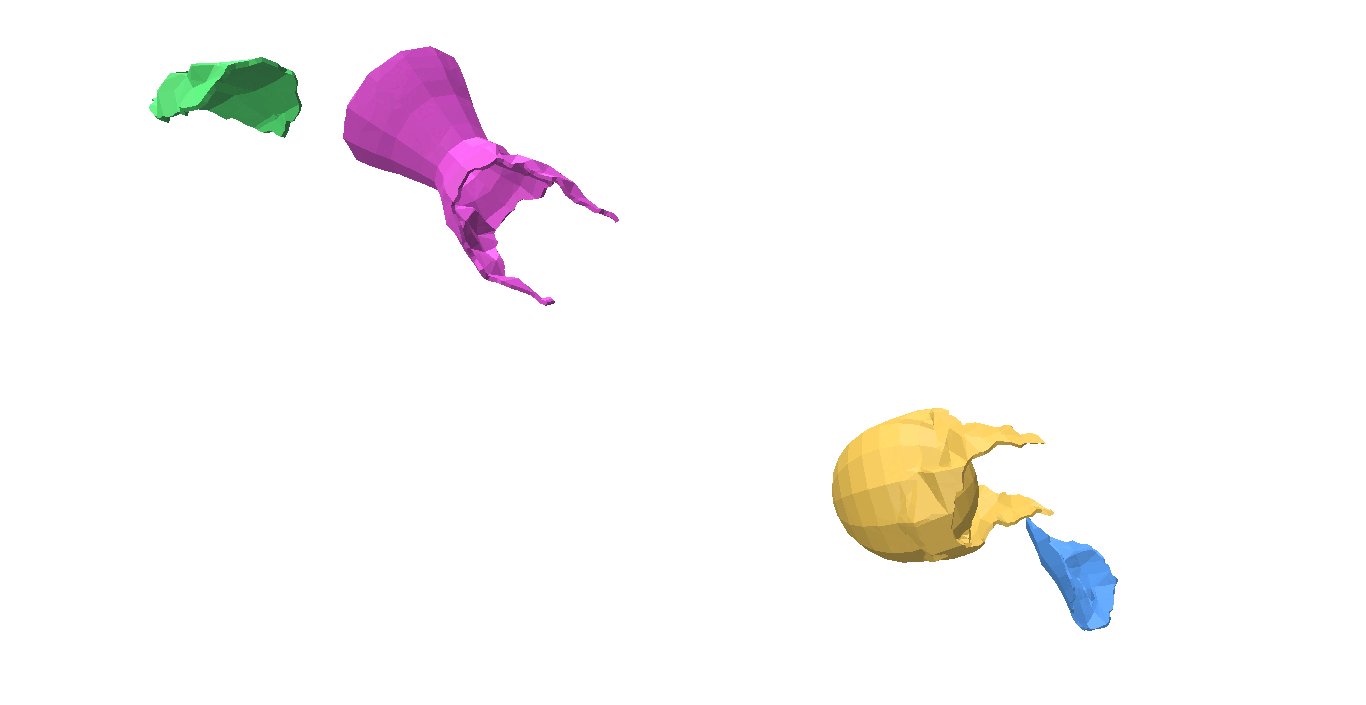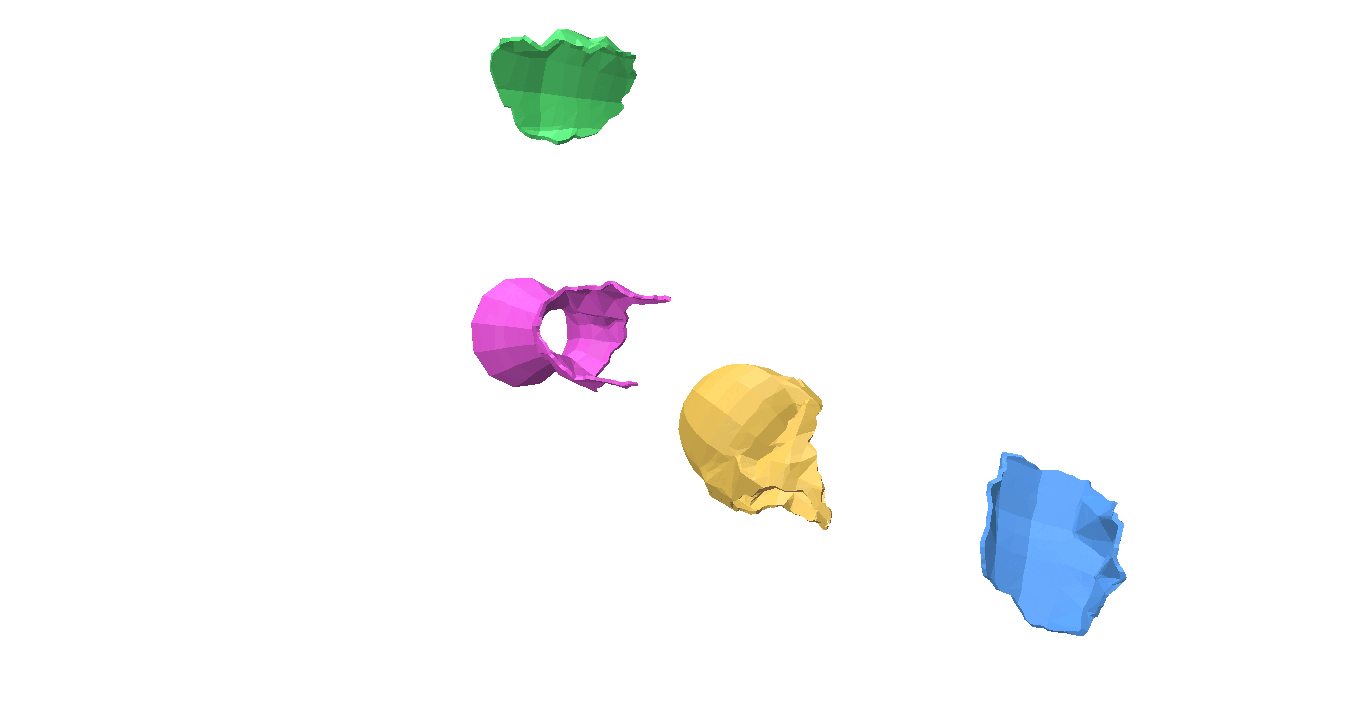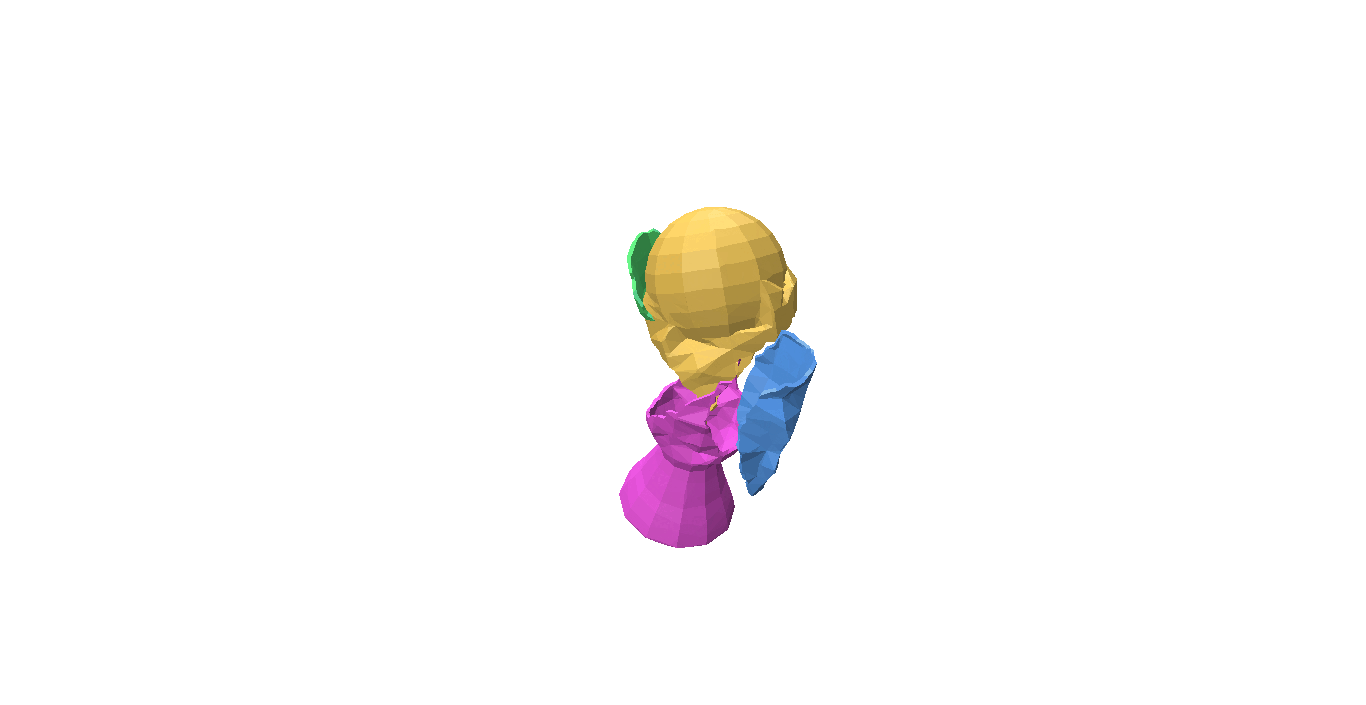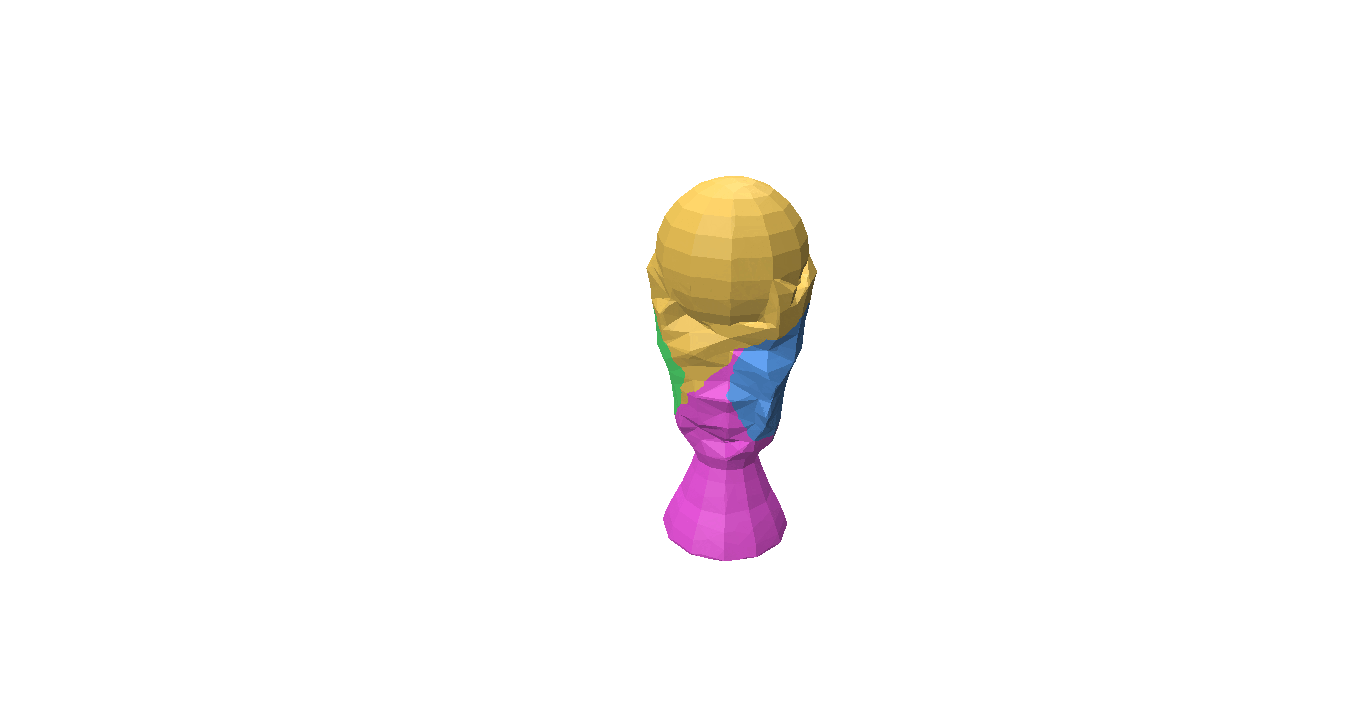
I. Introduction
In computer graphics, fracture simulation of everyday objects is a well-studied problem. Physics-based pre-fracture algorithms like Breaking Good [1] can be used to simulate how objects break down under different dynamic conditions. The inverse of this problem is geometric fracture assembly, where the task is to compose the components of a fractured object back into its original shape.
More concretely, we can formulate the fracture assembly task as a pose prediction problem. Given \(N\) mesh fractured pieces of an object, the goal is to predict a \(SE(3)\) pose for each fractured part. We can denote the predicted pose of the \(i_{th}\) fractured piece as \(p_i = \{(q_i, t_i) | q_i \in R^4, t_i \in R^3\}\), where \(q_i\) is a unit quaternion describing the rotation and \(t_i\) is the translation vector. We can apply the predicted pose to the vertices \(V_i\) of each fractured piece and get \(p_i(V_i) = q_i V_i q_i^{-1} + t_i\). The union of all of the pose-transformed pieces is our final assembly result, \(S = \bigcup p_i(V_i)\).
The goal of this project is to come up with an evaluation metric to compare different assembly algorithms and to host an open source challenge for the assembly task.
II. Rotation metric:
We will use unit quaternions \(q\) to represent rotations. Let’s assume for one of the pieces of the fracture, \(q_r\) is the true rotation and \(q_p\) is the predicted rotation. We might define a metric between two rotations as the Euclidean distance between two quaternions:
\(d(q_r, q_p) = ||q_r-q_p||^2\)
But a noteworthy property of quaternions is that two quaternions \(q\) and \(-q\) represent the same rotation. This can be verified as follows:
The rotation \(R\) related to quaternion \(q\) sends a vector \(v\) to the vector:
\(R(v) = qvq^{-1}\)
The rotation \(R’\) related to quaternion \(-q\) sends the vector \(v\) to the vector:
\begin{array} {lcl} R'(v) & = & (-q)v(-q)^{-1} \\ & = & (-1)^2 qvq^{-1} \\ & = & qvq^{-1} \end{array}
Which is the same as the rotation \(R\).
Directly using the Euclidean distance for quaternions would be ambiguous because the distance between the same rotations \(q\) and \(-q\) would be non-zero.
To alleviate this, we have to choose a sign convention for the quaternions. We choose the quaternions to always have a positive real part. When we encounter quaternions with negative real components, we flip its sign (which represents the same rotation). Then we can compare the quaternions using the usual \(L^2\) distance. This is the pseudo code for our rotation metric:
def rotation_metric(qr, qp):
if real(qr) < 0:
qr = -qr
if real(qp) < 0:
qp = -qp
return sum((qr-qp)**2)III. Translation Metric:
If \(t_r\) is the true translation and \(t_p\) is the predicted translation for one of our fractured pieces, we can directly use the \(L^2\) distance between the translation vectors as the translation metric:
\(d(t_r, t_q) = ||t_r – t_q||^2\)
IV. Relative rotation and translation:

Fig 1: Even when all the pieces are rotated or translated with respect to the ground truth, it can still be a valid shape assembly.
While evaluating a predicted pose we must be careful, because the predicted values can be very different from the ground truth but can still describe a valid shape assembly. This is illustrated in Fig 1: We can rotate and translate all the pieces together by a certain amount that will result in a large value for our \(L^2\) metric, although this is a perfect shape assembly.
We solve this problem by measuring all the rotations and translations relative to one of the fragmented pieces.
Let’s assume we have two pieces:
Piece 1: rotation \(q_1\), translation \(t_1\)
Piece 2: rotation \(q_2\), translation \(t_2\)
Then the relative rotation and translation of Piece 2, with respect to Piece 1, can be calculated as:
\(q_{rel} = q_1^{-1} q_2\)
\(t_{rel} = q_1^{-1} (t_2-t_1) q_1\)
For both ground truth and prediction, we can calculate the relative rotations and translations of all the parts with respect to a chosen piece. Then we can easily use the \(L^2\) metrics defined above for comparison. This won’t affect the metric if all the pieces are moved together.
V. Codalab Challenge
We started implementing a Codalab challenge to explore this problem in all its complexities. For this, we set up a server that implemented the previously mentioned metrics and also started designing the type of submissions we could do.
Our scripts consisted in a code to evaluate the submissions in the Codalab server, the reference data we used to perform the evaluation and a starter-kit that could be used by people that are starting in the competition.
VI. References
[1] Silvia Sellán, Jack Luong, Leticia Mattos Da Silva, Aravind Ramakrishnan, Yuchuan Yang, Alec Jacobson. “Breaking Good: Fracture Modes for Realtime Destruction”. ACM Transactions on Graphics 2022.
[2] Silvia Sellán, Yun-Chun Chen, Ziyi Wu, Animesh Garg, Alec Jacobson. “Breaking Bad: A Dataset for Geometric Fracture and Reassembly”. Neural Information Processing Systems 2022.