Random Meshes

Fellows: Aditya Abhyankar, Munshi Sanowar Raihan, Shanthika Naik, Bereket Faltamo, Daniel Perazzo

Volunteer: Despoina Paschalidou

Mentor: Nicholas Sharp

I. Introduction

Triangular and tetrahedral meshes are central to geometry, we use them to represent shapes, and as bases to compute with. Many numerical algorithms only actually work well on meshes that have nicely-shaped triangles/tetrahedra, so we try very hard to generate meshes which simultaneously:

1.  Represent the desired shape
2.  Have nicely-shaped elements and 
3. Perfectly interlock to cover the domain with no gaps or overlaps. 

Yet, is point (3) really that important? What if instead we just sampled a soup of random nicely-shaped triangles, and didn’t worry about whether they fit together? 

In this project we explore several strategies for generating such random meshes, and evaluate their effectiveness. 

II. Algorithms

II.1. Triangle Sampling

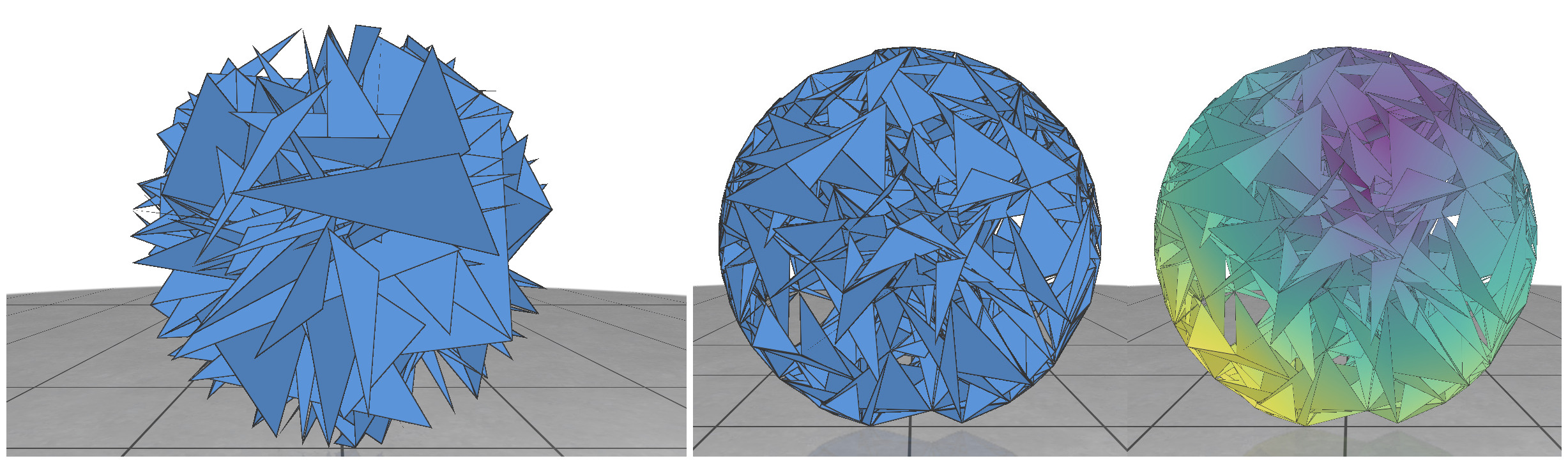
In random meshing, we are given the boundary of a shape (e.g. the polygon outline of a 2D figure) and the task is to generate random meshes to tessellate the interior. Here, we will focus mainly on the planar case, where we generate triangles with 2D vertex positions. We will test the generated meshes by running the Heat Method [2], a simulation-based algorithm for computing distance within a shape. The very first shape we tried to tessellate is a circular disk.

Since a circle is a convex shape, we can choose three random points inside the circle and any triangle is guaranteed to stay within the shape. But generating isolated triangles like these is not a good strategy, because downstream algorithms like the heat method rely on shared vertices to communicate across the mesh. Without shared vertices, it is equivalent to running the algorithm individually on a bunch of separate triangles one at a time.

Next strategy: At each vertex, consider generating n random triangles that are connected to other vertices within a certain radius. This ensures that the generated triangles share the same vertex entries. Even though these random triangles have many gaps and intersections, many algorithms are actually perfectly well-defined on such a mesh. To our surprise, the heat method was able to generate reasonable results even with these random soup of triangles (Fig 1).

II.2. Non-Convex Shapes

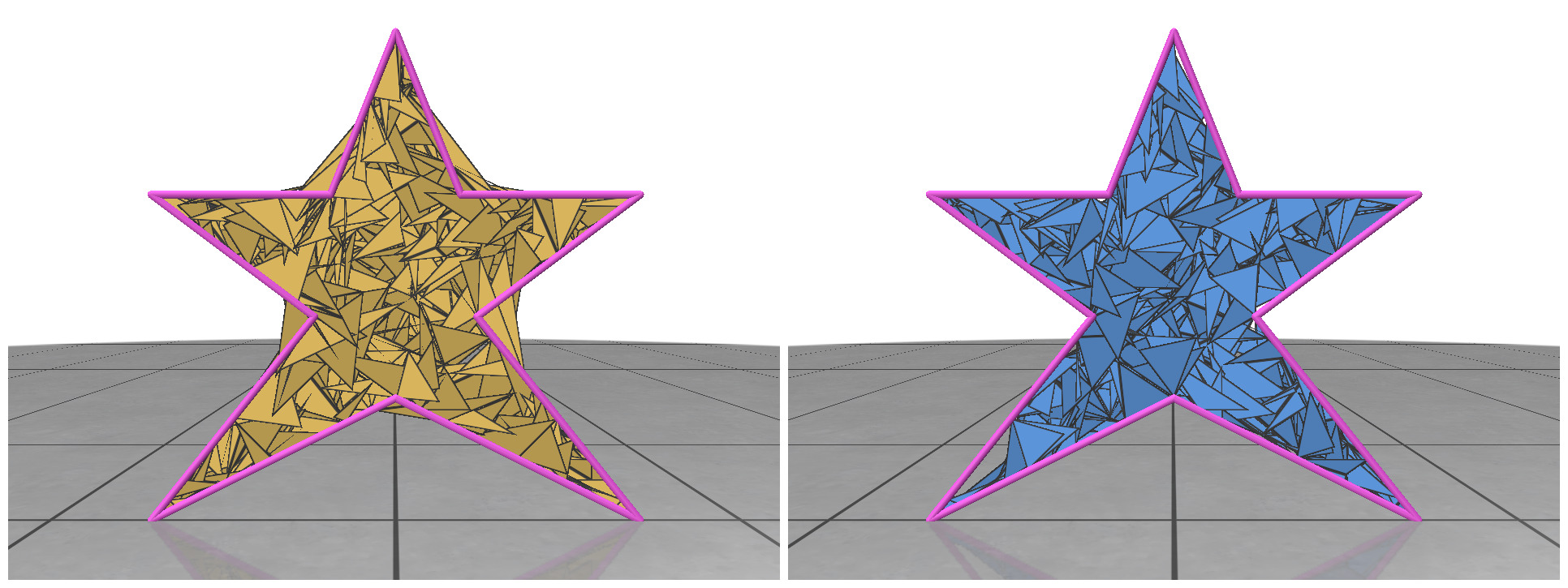
For non-convex shapes, if we try to connect any three points within the polygon, some of the triangles might fall outside of our 2D boundary. This is illustrated in Fig 2 (left). To circumvent this problem, we can do rejection sampling of the triangles. Every time we generate a new triangle, we need to test whether it is completely contained within the boundary of our polygon. If it’s not, we reject it from our face list and sample another one. After rejection, the random meshes seem to nicely follow the boundary. Rejection sampling makes our meshing algorithm a little slower, but it’s necessary to handle non-convex shapes.

II.3. Triangle Size

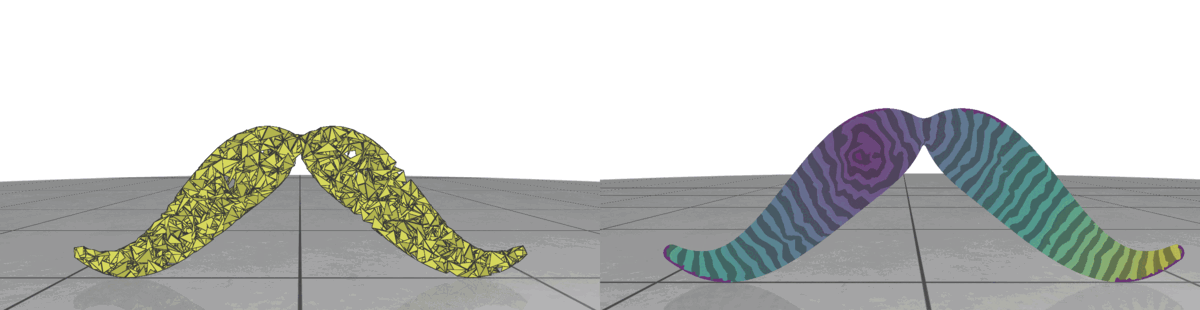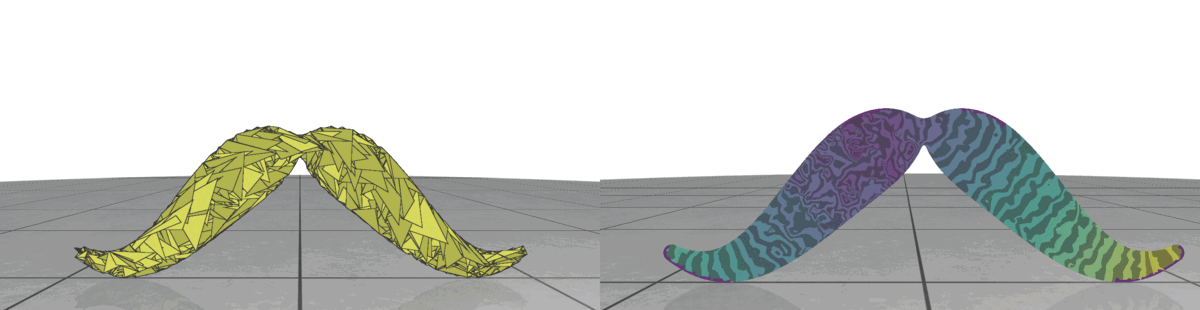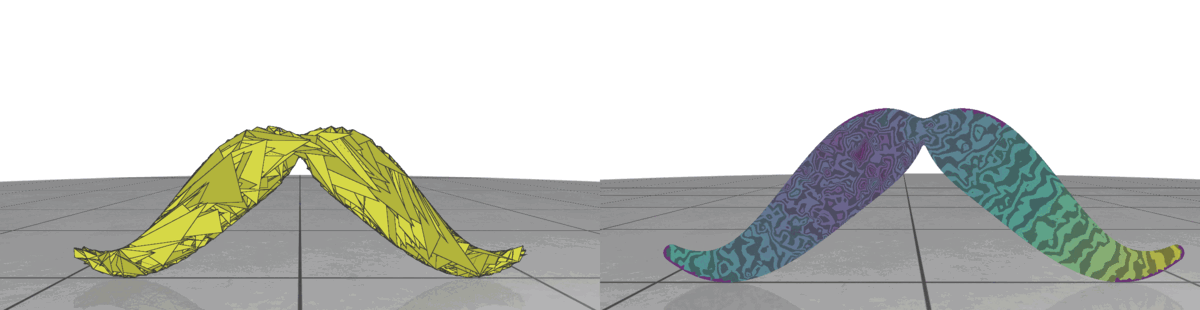
In random meshes, we find that the performance of the heat geodesic method is dependent on the size of the triangles. Since we are generating triangles by sampling points within a radius, we can make the triangles smaller or larger by controlling the radius of the circle. With decreasing triangle size, the distance computed by the heat method becomes more accurate. This is illustrated in Fig 3: as the triangles become smaller, the isolines look more precise. The number of triangles are kept fixed in all cases.

III. Visualizations and results

We created an interface to aid in the task of drawing different polygon shapes for visualization. As can be seen below, an example of a shape:

We can use one of our algorithms to plot various types of meshes with the distance function drawn by the heat equation. We put the visualization of these meshes bellow, where the leftmost is the mesh using Delaunay triangulation, the rightmost using random triangles and the center being using Delaunay triangulation but using the faces from the Delaunay triangulation for a better visualization.

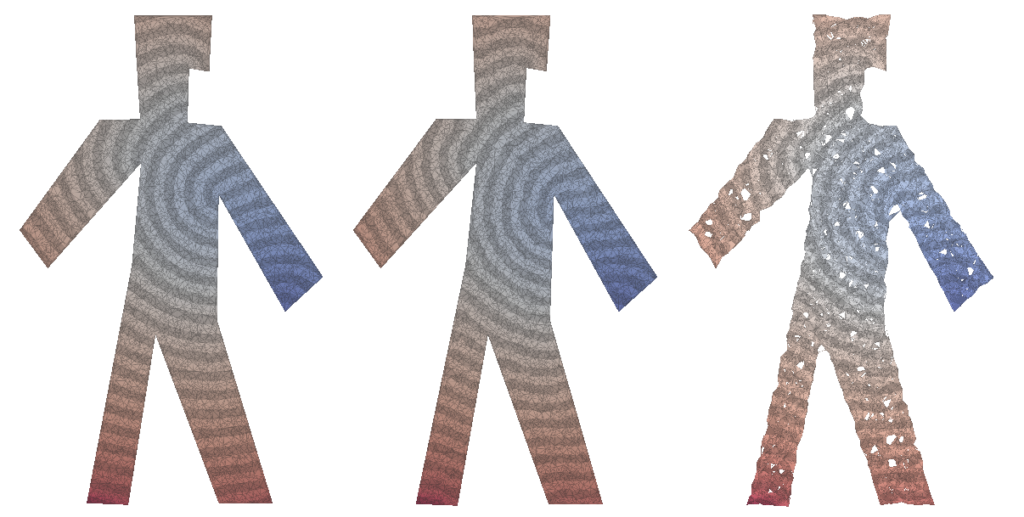
In this case, with 5000 points sampled randomly, we have an error of 0.0002 compared with the values for the distance function compared with using the heat method.

IV. An Attempt at Random Walk Meshing

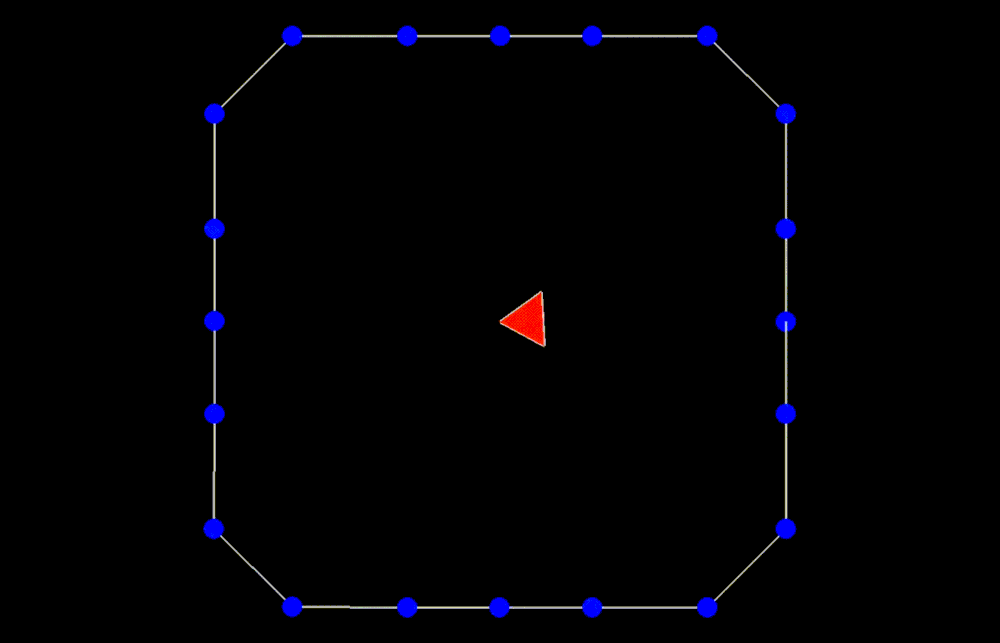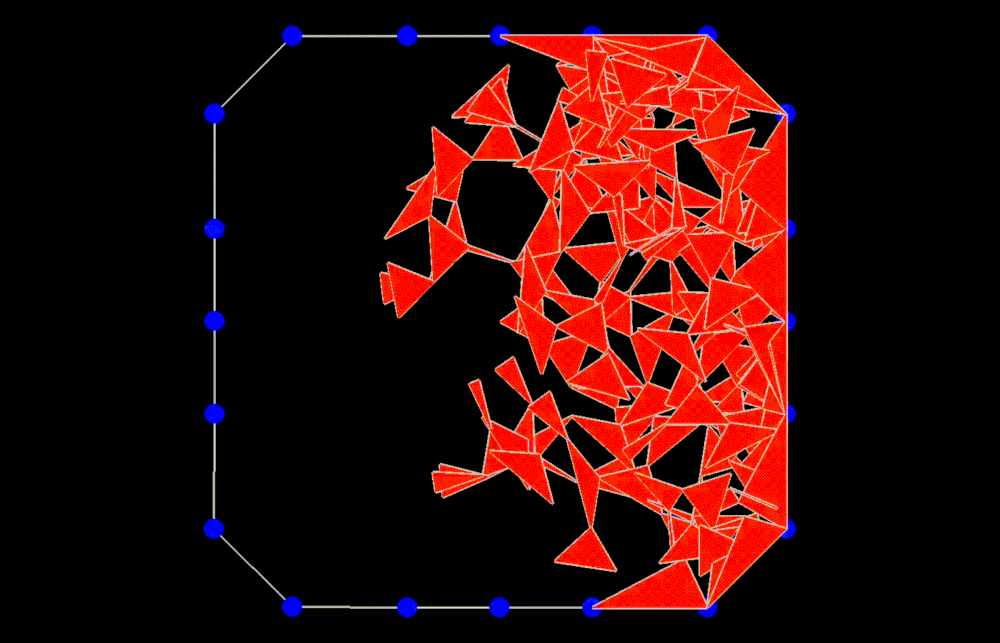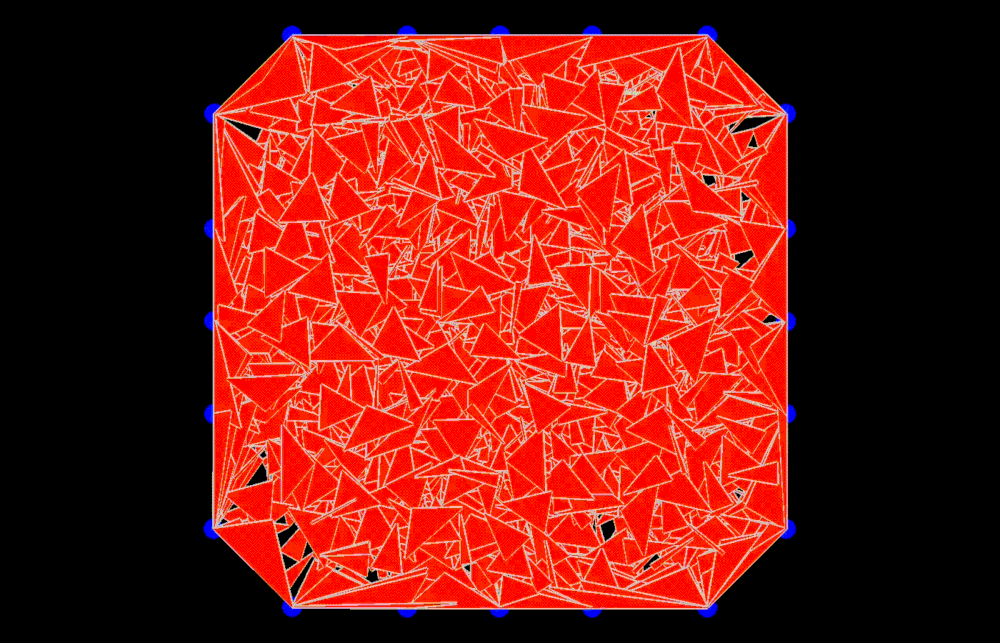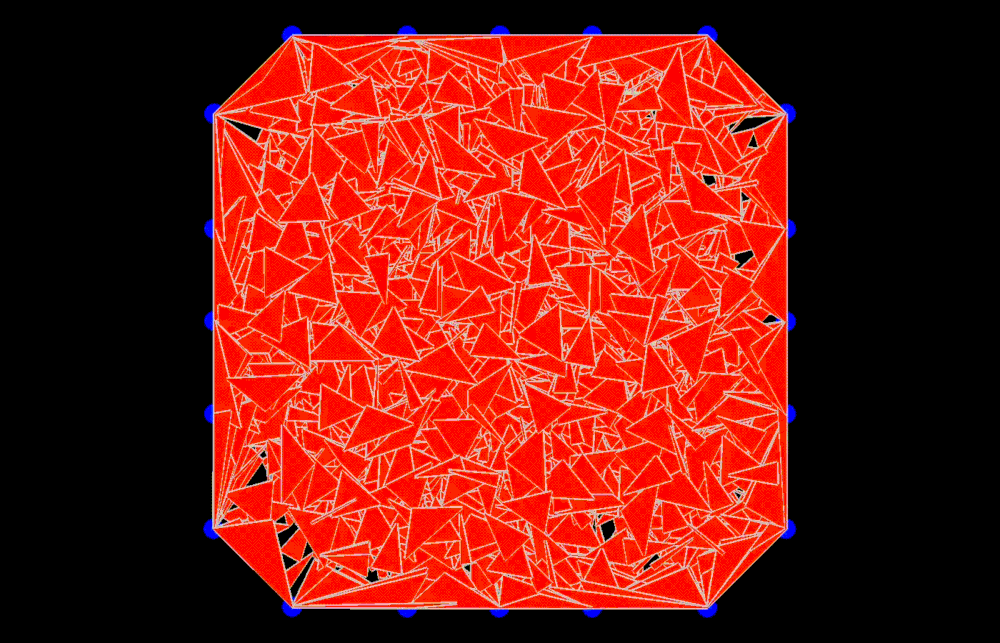
Another interesting meshing idea is spawning a single vertex somewhere in the interior of the shape, and then iteratively “growing” the mesh from there in the style of a random walk. At each iteration, every leaf vertex randomly spawns two more child vertices on the circumference of a circle surrounding it, which are used to form a new face. If any such spawning circle intersects with the boundary of the shape, we simply use the two vertices of the closest boundary edge instead to form the new face. We tried various types of random walk strategies, such as using correlated random walks with various correlation settings to mitigate clustering at the source vertex. 

While this produced an interesting single component random mesh, the sparse connectivity made it a bad algorithm for the heat method, as triangle sequences that swiveled back around in the direction of the source vertex diffused heat backwards in that direction too.

This caused the distance computations to be inaccurate and rendered the other methods superior. We would like to explore this approach further though, as it might prove useful for other use-cases like physics simulations and area approximations. Random walks are very well studied in probability literature too, so deriving theoretical results for such algorithms seems like a very principled task.

V. Structure in Randomness

While sampling triangles within a radius gave a reasonable results upon calculating geodesic distance, we tried exploring ways to make it more structured. One such method we came with is grid sampling with triangulation within a neighborhood. The steps are as follows:

1. Uniformly sample points within a square grid enclosing the entire shape.
2. Eliminate points outside that fall out of the desired shape.
3. For each vertex within the shape, form a fan of triangles with its 1 ring neighborhood vertices.

These are the geodesic isolines on the triangular mesh obtained using the above method.

VI. Conclusion and Future Work

We present some examples of our random computation method working on 2D meshes for various different shapes. Aside from refining our algorithms and performing more experiments, one interesting avenue would be to perform experiments with tetrahedralization on 3D shapes. We have also done simple tests with current state-of-the-art tetrahedralization algorithms [3], the results are shown below. So, for future work, this would be a really interesting avenue. Another interesting avenue for theoretical work regarding random walk meshing would be computing how the density of triangles varies with iteration count and various degrees of correlation.

VII. References

[1] Shewchuk, Jonathan Richard. “Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator.” Workshop on applied computational geometry. Berlin, Heidelberg: Springer Berlin Heidelberg, 1996.

[2] Crane, Keenan, Clarisse Weischedel, and Max Wardetzky. “The heat method for distance computation.” Communications of the ACM 60.11 (2017): 90-99.

[3] Hu, Yixin, et al. “Tetrahedral meshing in the wild.” ACM Trans. Graph. 37.4 (2018): 60-1.

[4] Hu, Yixin, et al. “Fast tetrahedral meshing in the wild.” ACM Transactions on Graphics (TOG) 39.4 (2020): 117-1.