Students: Gabriele Dominici, Daniel Perazzo, Munshi Sanowar Raihan, Biruk Abere, Sana Arastehfar
TA: Jiri Mirnacik
Mentor: Tongzhou Wang
Introduction
In reinforcement learning (RL), an agent is placed in an environment, and is required to complete some task from a starting state. Traditionally, RL is often studied under the single-task setting, where the agent is taught to do one task and one task only. However, multi-task agents are much more general and useful. A robot that knows to do all household tasks is much more valuable than one that only opens the door. In particular, many useful tasks of interest are goal-reaching tasks, i.e., reaching a specific given goal state from any starting state.
Each RL environment implicitly defines a distance-like geometry on its states:
“distance”(state A, state B) := #steps needed for an agent to go from state A to state B.
Such a distance-like object is called a quasimetric. It is a relaxation of the metric/distance function in that it can be asymmetrical (i.e., d(x,y) != d(y,x) in general). For example,
- Going up a hill is harder than going down the hill.
- Dynamic systems that model velocity are generally asymmetrical (irreversible).
Asymmetrical & irreversible dynamics occur frequently in games, e.g., this ice-sliding puzzle.
(Game: Professor Layton and Pandora’s Diabolical Box)
This quasimetric function captures how the environment evolves with respect to agent behavior. In fact, for any environment, its quasimetric is exactly what is needed to efficiently solve all goal-reaching tasks.
Quasimetric RL (QRL) is a goal-reaching RL method via learning this quasimetric function. By training on local transitions (state, action, next state), QRL learns to embed states into a latent representation space, where the latent quasimetric distance coincides with the quasimetric geometry for the environment. See https://www.tongzhouwang.info/quasimetric_rl/ for details.
The QRL paper explores the control capabilities of the learned quasimetric function, but not the representation learning aspects. In this project, we aim to probe the properties of learned latent spaces, which have a quasimetric geometry that is trained to model the environment geometry.
Setup. We design grid-world-like environments, and use an provided implementation of QRL in PyTorch to train QRL quasimetric functions. Afterwards, we perform qualitative and visual analyses on the learned latent space.
Environments
Gridworld with directions
In reinforcement learning for the Markov decision process, the agent has access to the internal state of the world. When the agent takes an action, the environment changes accordingly and returns the new state. In our case, we try to simulate a robot trying to reach a goal.
Our agent has only three actions: go forward, turn right and turn left. We assume that the agent has reached the goal if it is around the goal with a small margin of error. For simplicity, we fix the initial position and the goal position. We set the angular velocity and the step size to be fixed for the robot.
The environment returns to the agent the position it is currently in, and the vector direction the robot is currently facing. Following the example in the original QRL paper, we have a constant reward of -1 for the agent which encourages the agent to reach the goal as quickly as possible.
Training
For this project, we tested QRL on the aforementioned environments, where we obtained some interesting results. Firstly, we performed an offline version of QRL using only a critic network. For this setting, we used a dataset of trajectories created by actors performing a random trajectory. This random trajectory is then loaded when training starts.As shown in the figure in the previous section, we have a robot performing a random trajectory.
We trained in QRL varying the parameters for training the neural network. Using QRL we let the network train for various steps, as can be seen below:
After performing this training we analysed what would the agent learn, however, unfortunately, it seems that the agent is stuck, as can be seen in the figure below:
To get a better understanding of the problem, we performed some experiments using A2C implementation from stable_baselines. Instead of using the angle set-up as mentioned early, we used a setting where we return the angle directly. We also performed various runs, ~10 for A2C and always testing the trajectories. Although there were some runs that A2C did not manage to find the right trajectory, on some it did. We show the best results bellow:
We also performed some tests varying the parameters for quasimetric learning and inserting an intermediary state for the agent to reach the goal. After varying some parameters, including batch size and the coordinate space the agent is traversing. The improved results can be seen bellow, where the agents manage to reach the goal. Also, instead of, during the visualization, instead of using a greedy approach we instead use a categorical distribution, varying a temperature parameter to make it more random:
These results were preliminary and we will not analyze these results for the next section.
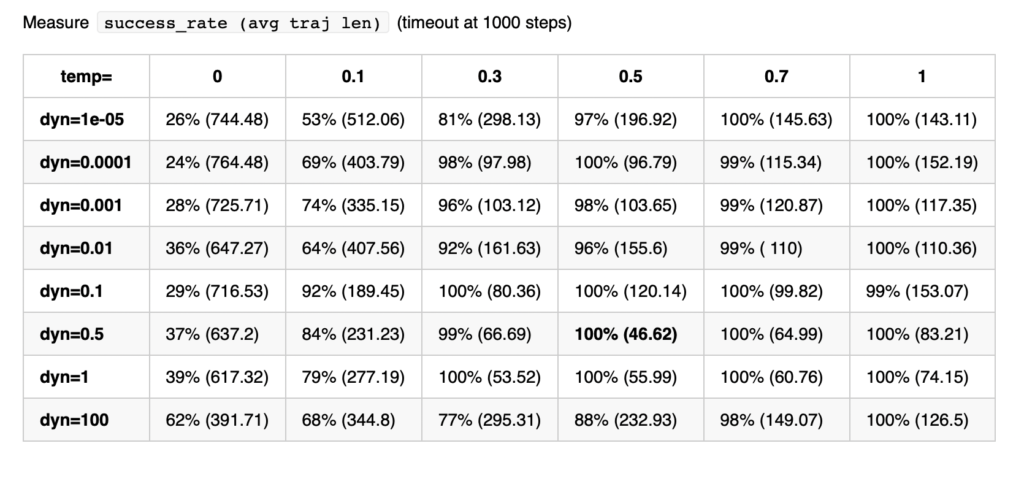
We also performed an analysis on different settings, using different weights for our dynamic loss and and varying the previously mentioned temperature parameter. The table is shown bellow
Analyses
As previously said, we inspect the latent space learnt by the neural network to represent each state. In such a manner, it would be possible to inspect how the model reasons about the environment and the task.
To do so, we sampled via a grid of parameters the state space of the Gridworld with directions environment. The grid was computed across 50 x values, 50 y values and 16 angle values equally separated. Then, we stored the latent representation computed by the model for each state and applied a t-SNE dimensionality reduction to qualitative evaluate the latent space referred to the state space.
Figure 6: t-SNE representation of the latent space of the state space. The color represents the normalized predicted quasimetric distance between that state and the goal (red dot).
Figure 6 shows how these latent spaces learned by the model are meaningful with respect to the predicted quasimetric distance between two states. Inspecting it more in depth, it is possible to see how it also has some properties in this environment. Mostly, if you move along the x-axis in the reduced space, you advance in the y-axis in the env with different angles, while if you move along the y-axis in the reduced space, you advance in the x-axis in the environment. In addition, we believe that this behavior would also be present in other environments, but it needs further analysis.
We also inspect the latent space learnt at different levels of the network (e.g. after including the possible actions and after the encoder in the quasimetric network), and all of them have similar representations.
Conclusion & Future directions
Even in basic environments with limited action spaces, understanding the decision-making of agents with policies learned by neural networks can be challenging. Visualization and analysis of the learned latent space provide useful insights, but they require careful interpretation as results can be misleading.
As quasimetric learning is a nuanced topic, many problems from this week remain open and there are several interesting directions to pursue after these initial experiments:
- Investigate the performance of quasimetric learning in various environments. What general properties of the environment are favorable for this approach?
- Analyze world-models and multi-step planning. In this project, we examined only a 1-step greedy strategy.
- Formulate and analyze quasimetric learning within a multi-environment context.
- Design and evaluate more intricate environments suitable for real robot control