Tag: PDEs

Categories
Research

Multigrid Solver for Curved Surfaces

Video 1: Numerical solution of the heat equation on curved meshes using a geometric multigrid solver.

By SGI Fellows:  Anna Cole, Francisco Unai Caja López, Matheus da Silva Araujo, Hossam Mohamed Saeed

Mentor: Paul Kry

Volunteers: Leticia Mattos Da Silva and Erik Amézquita

I. Introduction

This technical report describes a follow-up to our previous post. One of the original goals of the project was to apply successive self-parameterization to solve differential equations on curved surfaces leveraging a multigrid solver based on Liu et al. 2021. This post reports the results obtained throughout the summer to achieve this objective and wraps-up the project. Video 1 shows an animation of heat diffusion, obtained by solving the heat equation on surface meshes using the geometric multigrid solver.

II. Partial Differential Equations

Partial differential equations (PDEs) are equations that relate multiple independent variables and their partial derivatives. In graphics and animation applications, PDEs usually involve time derivatives and spatial derivatives, e.g., the motion of an object in 3D space through time described by a function \(f(x, y, z, t)\). Frequently, a set of relationships between partial derivatives of a function is given and the goal is to find functions \(f\) satisfying these relationships.

To more easily study and analyze these equations, it is possible to classify them according to the physical phenomena they describe, which are briefly summarized below. Solomon 2015 and Heath 2018 provide extensive details on partial differential equations for those interested in more in-depth discussions on the topic.

Elliptic PDEs are PDEs that describe systems that have already reached an equilibrium (or steady) state. One example of elliptic PDE is the Laplace equation, given by \(\bigtriangleup \mathbf{u} = \mathbf{0}\). Intuitively, starting with values known only at the boundary of the domain (i.e., the boundary conditions), this equation finds a function \(\mathbf{u}\) such that the values in the interior of the domain smoothly interpolate the boundary values. Figure 1 illustrates this description.

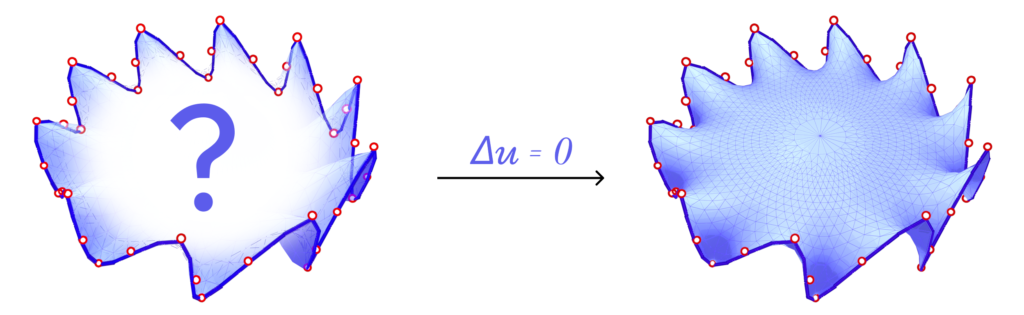
Figure 1: Given boundary conditions, the Laplace Equation is satisfied by a function that smoothly interpolates it to the interior.

Parabolic PDEs are equations that describe systems that are evolving towards an equilibrium state, usually related to dissipative physical behaviour. The canonical example of a parabolic PDE is the heat equation, defined as \(\frac{\mathrm{d}}{\mathrm{dt}} \mathbf{u} = \bigtriangleup \mathbf{u}\). The function \(\mathbf{u}\) describes how heat flows with time over the domain, given an initial heat distribution that describes the boundary conditions. This behaviour can be visualized in Animation 1.

Animation 1: Given an initial heat distribution, the heat equation describes how heat flows over the surface as time progresses, until a steady state is reached.

Finally, hyperbolic PDEs describe conservative systems that are not evolving towards an equilibrium state. The wave equation, described by \(\frac{\mathrm{d}^2}{\mathrm{dt^{2}}} \mathbf{u} = \bigtriangleup \mathbf{u}\), is the typical example of a hyperbolic PDE. In this case, the function \(\mathbf{u}\) characterizes the motion of waves across elastic materials or the motion of waves across the surface of water. Animation 2 provides a visual illustration of this phenomenon. One striking difference between the wave equation and the heat equation is that for the former it is not enough to specify initial conditions for \(\mathbf{u}\) at time \(t = 0\); it is also necessary to define initial conditions for the derivatives \(\mathbf{\frac{\mathrm{d}}{\mathbf{dt}} \mathbf{u}}\) at time \(t = 0\).

Animation 2: Given initial boundary conditions for both the function and its first derivative, the wave equation describes the propagation of a wave through time.

In this project, we restricted the implementation to solving the heat diffusion equations on curved triangle meshes (see Crane et al. 2013). This leads to the following time discretization using a backward Euler step:

\(\begin{equation} \frac{\mathrm{d}}{\mathrm{dt}} \mathbf{u} = \bigtriangleup \mathbf{u} \rightarrow (\mathbf{I} – t\mathbf{L}) \mathbf{u}_{t} = \mathbf{u}_{0} \end{equation}\)

where \(\mathbf{u}_{0}\) is the initial heat distribution and \(\mathbf{L}\) is the Laplacian.

To spatially discretize the equation, we used the cotan-Laplacian \(\mathbf{L}\) discretized at a vertex \(i\):

\(\begin{equation} (\mathbf{L}u){i} = \frac{1}{2 A_{i}} \sum_{j \in \mathcal{N}_{i}} \left(\cot \alpha_{ij} + \cot \beta_{ij} \right) \left(u_{j} – u_{i} \right) \end{equation}\)

where \(A_{i}\) is one-third of the sum of the areas of all the triangles incident to vertex \(i\), \(\mathcal{N}_{i}\) denotes the set of adjacent vertices, and \(\alpha_{ij}, \beta_{ij}\) are the angles that oppose the edge \(e_{ij}\) connecting vertex \(i\) to its neighbor \(j\). The result is a linear system \(\mathbf{A}\mathbf{x} = \mathbf{b}\), where \(\mathbf{A} = \mathbf{I} – t\mathbf{L}\) and \(\mathbf{b} = \mathbf{u}_{0}\). This linear system can be solved numerically.

III. Multigrid Method

There is a large variety of methods to numerically solve PDEs. After choosing time and spatial discretization, the PDE may be solved as a linear system. To that end, it is possible to apply a direct solver (e.g., LU decomposition or Cholesky factorization) to find the solution. These methods are exact in the sense that they provide an exact solution in a finite number of steps. One disadvantage of direct solvers approach is that it may be too expensive to frequently recompute the matrix decomposition in cases where the system of equations requires updates. Iterative methods (e.g., Gauss-Seidel and Jacobi) provide an efficient alternative, but at the cost of providing only approximate solutions and having poor rates of convergence. Multigrid methods attempt to improve the convergence of iterative solvers by creating a hierarchy of meshes and solving the linear system in a hierarchical manner.

Iterative methods usually rapidly remove high-frequency errors, but slowly reduce low-frequency errors. This significantly affects the rate of convergence. The key observation of multigrid solvers is that low-frequency errors on the domain where the solution is defined (i.e., a grid or mesh) correspond to high-frequency errors on a \emph{coarser} domain. Hence, by simplifying the domain of the solution and transferring the errors from the original domain to a simplified one, an iterative solver can be used again on the coarse domain. The final result is that both high-frequency and low-frequency errors will be reduced in the original domain. See Solomon 2015 and Heath 2018 for details on numerical solutions for partial differential equations, and Botsch et al. 2010 for a discussion of multigrid methods applied to geometry processing in particular.

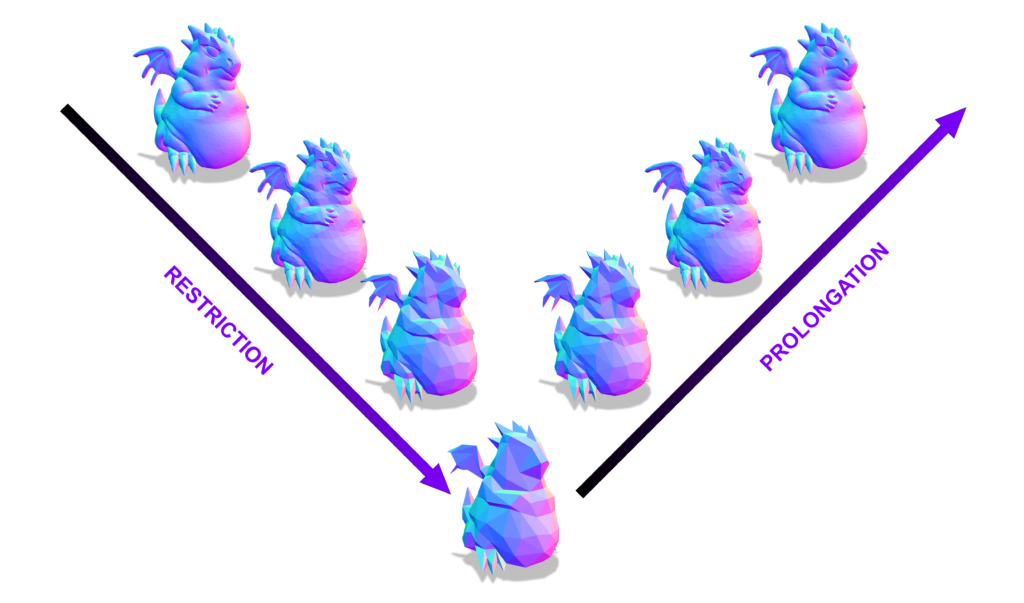
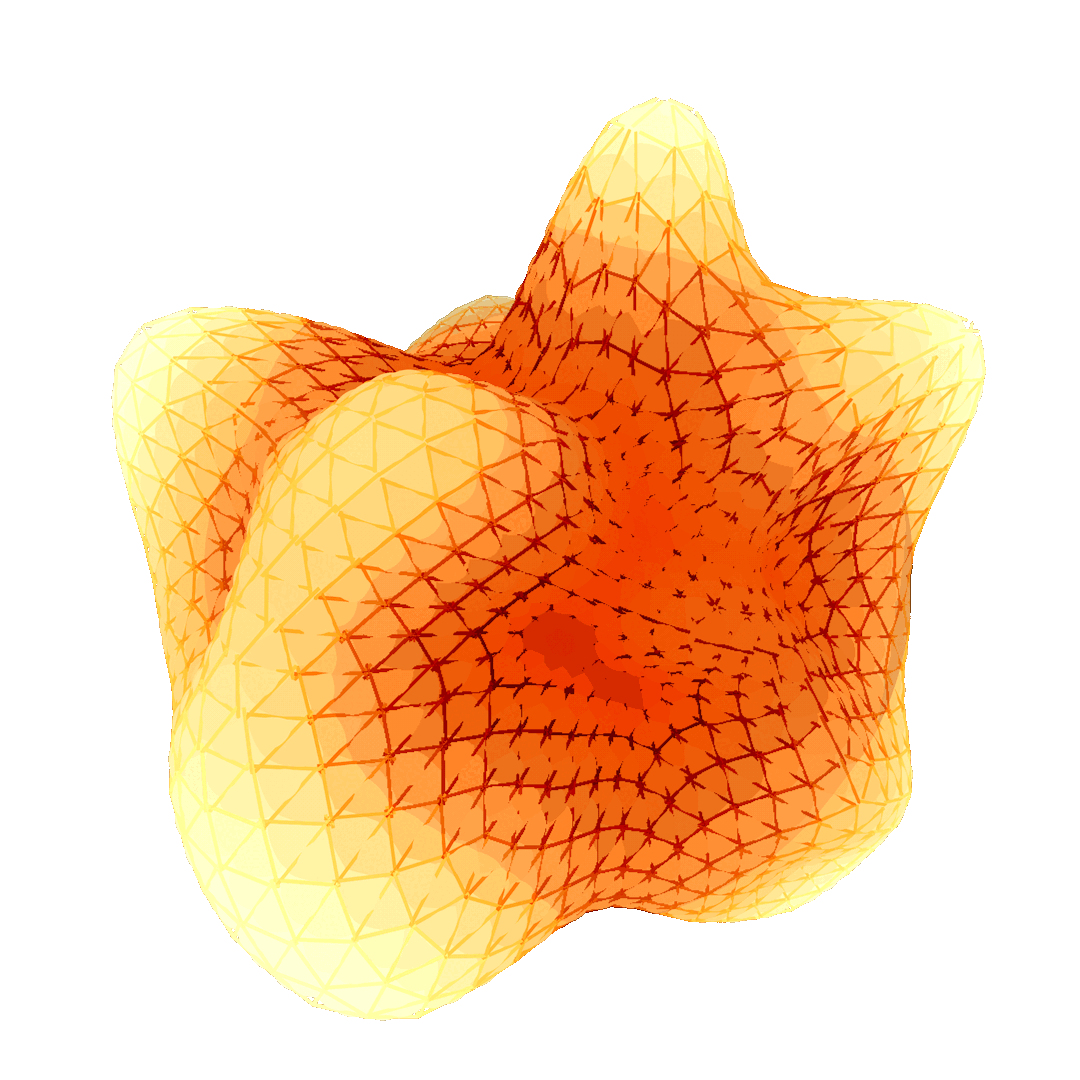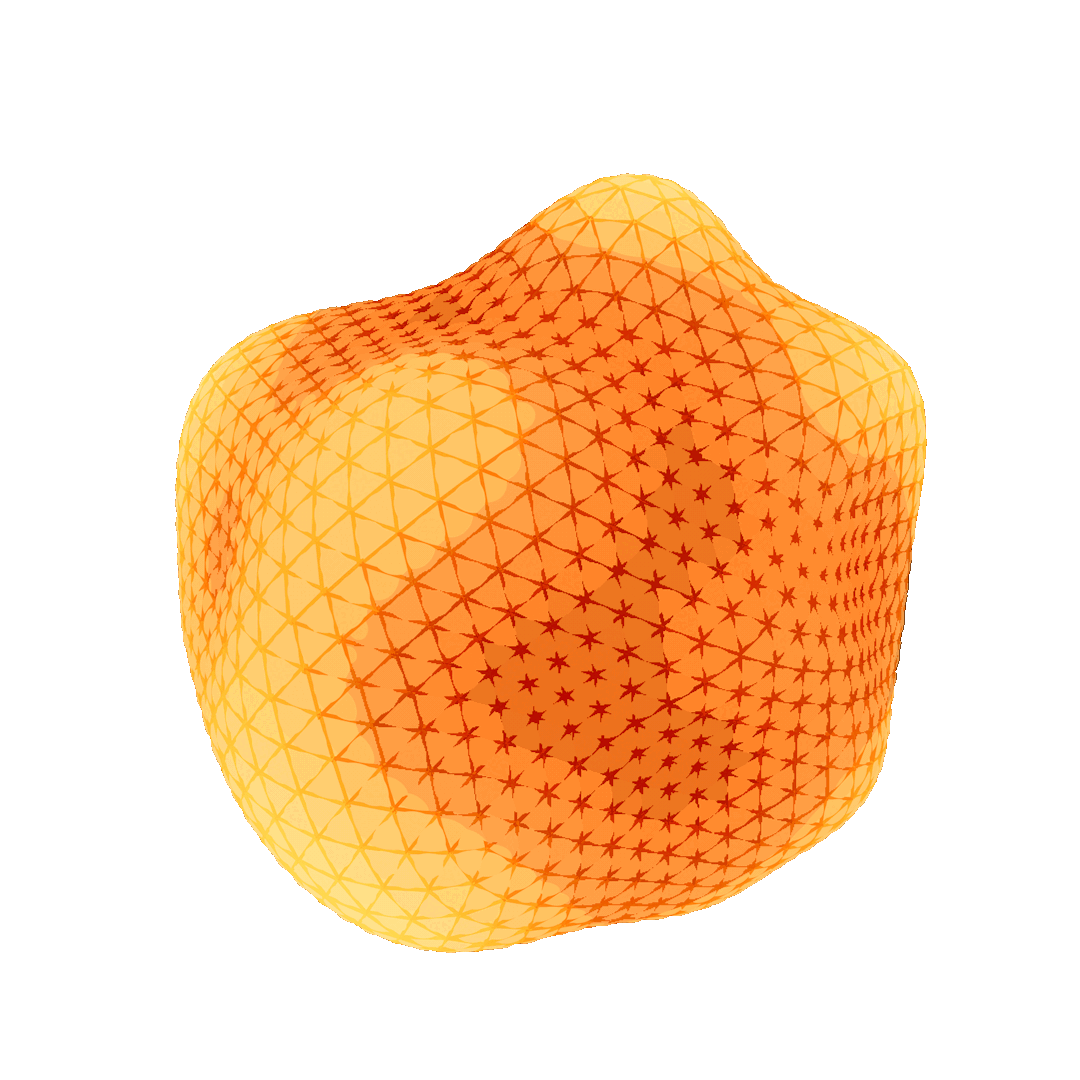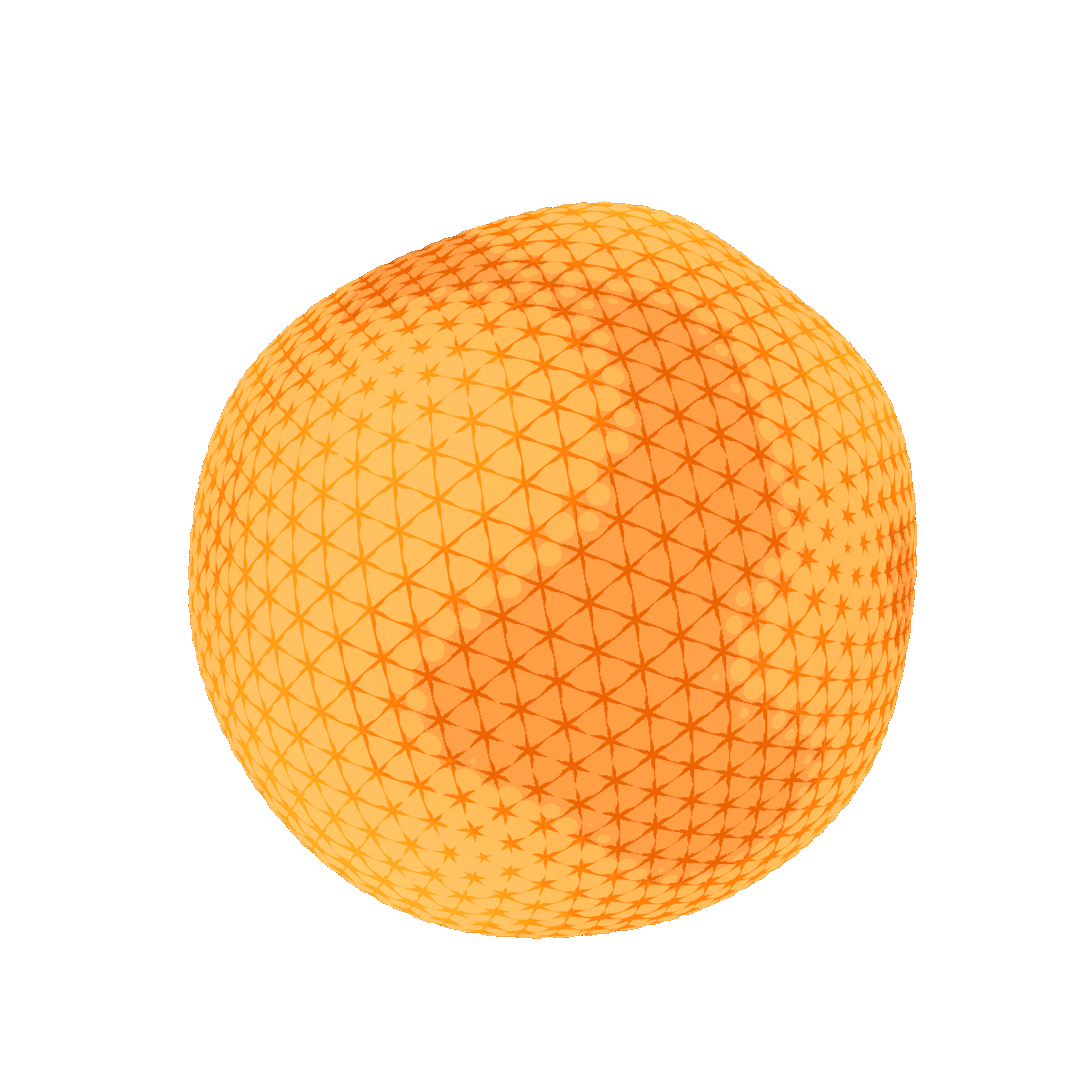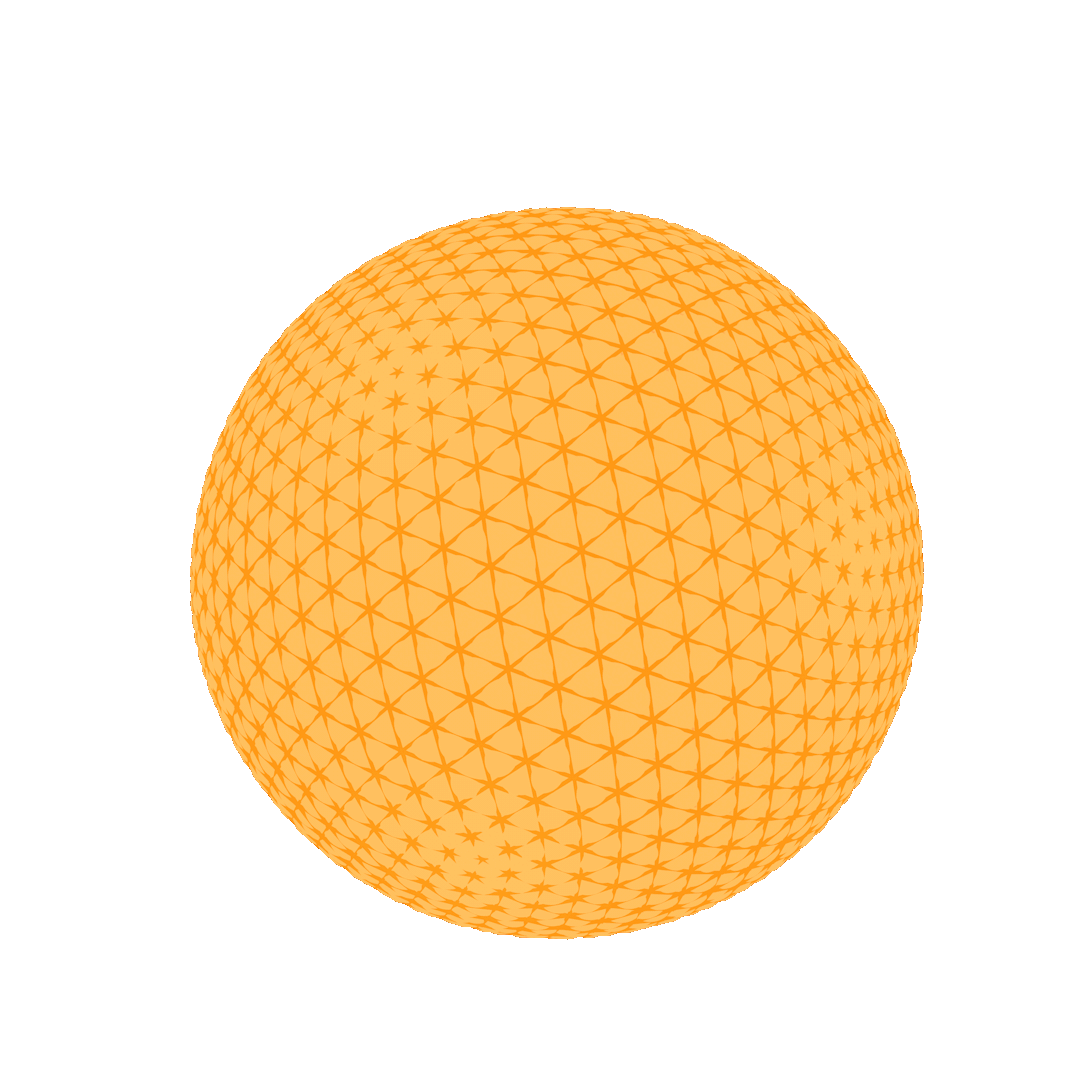
Figure 2: Restriction operators transfer residuals from fine to coarse meshes, while prolongation operators transfer the solution back from coarse to fine meshes. A direct solver is applied at the coarsest level of the hierarchy.

To transfer residuals from a fine level to a coarse level, a restriction operator must be defined, while the transfer from a coarse level to a fine level requires a prolongation operator that interpolates the solution found on coarse meshes to fine ones. This concept is illustrated in Figure 2 through a cycle of restriction and prolongation operators applied to a hierarchy of meshes. The method requires both a hierarchy of grids or meshes and a suitable mapping between successive levels of the hierarchy. For structured domains, such as grids, restriction and prolongation operators are well-established due to the regularity of the domain (Brandt 1977). For unstructured domains, such as curved surface meshes, it is harder to define a mapping between different levels of the hierarchy. To this end, Liu et al. 2021 proposes an intrinsic prolongation operator based on the successive self-parameterization of Liu et al. 2020, discussed in our previous report. To summarize, successive self-parameterization creates a bijective mapping between successive levels of the hierarchy, making it feasible to transfer back-and-forth the residuals in both directions (fine-to-coarse and coarse-to-fine). To achieve this, quadric mesh simplification is used to create the hierarchy of meshes and conformal parameterization is employed to uniquely correspond points on successive hierarchical levels.

Using the intrinsic prolongation operator matrix \(\mathbf{P}_{h}\) and the restriction operator matrix \(\mathbf{R} = \mathbf{P}_{h}^{T}\) for a level \(h\) of the hierarchy, where each level of the hierarchy has different prolongation/restriction matrices, the multigrid algorithm can be summarized as follows (Liu et al. 2021, Heath 2018):

  1. Inputs: a system matrix \(\mathbf{A}\), the right-hand side of the linear system \(\mathbf{b}\), and a sequence of prolongation-restriction operators for the hierarchy.
  2. Pre-Smoothing: at level \(h\) of the hierarchy, compute an approximate solution \(\hat{\mathbf{x}}\) for the linear system \(\mathbf{A} \mathbf{x} = \mathbf{b}\) using a smoother (for instance, the Gauss-Seidel solver). A small number of iterations should be used in the smoothing process.
  3. Compute the residual and transfer it to the next level of the hierarchy (a coarse mesh): \(\mathbf{r} = \mathbf{P}_{h + 1}^{T} \left(\mathbf{b} – \mathbf{A} \hat{\mathbf{x}} \right)\). The system matrix of the next level is given by \(\mathbf{\hat{A}} = \mathbf{P}_{h+1}^{T}\mathbf{A}\mathbf{P}_{h+1}\).
  4. Recursively apply the method using the residual found in the previous step and return the solution \(\mathbf{c}_{h+1}\) found in the next level of the hierarchy. As the base case, a direct solver can be used at the coarsest level of the hierarchy. This should be efficient, since the system to be solved will be small at the coarsest level.
  5. Interpolate the results found by the method at the next level of the hierarchy using the prolongation operator: \(\mathbf{x}’ = \mathbf{P}_{h + 1} \mathbf{c}_{h+1}\).
  6. Post-Smoothing: apply a small number of iterations of a smoother (e.g., the Gauss-Seidel solver) on the solution found in the previous step.

For the sake of completeness, the multigrid solver described is more specifically an example of a geometric multigrid method, since the system was simplified using the geometry of the mesh or domain. In contrast, an algebraic multigrid method constructs a hierarchy from the system matrix without additional geometric information. Moreover, the hierarchy traversal described (going from finest to coarsest and back to finest) is known as a V-cycle multigrid, but there are many possible variants such as W-cycle multigrid, full multigrid and cascading multigrid. Again, we refer the reader to Heath 2018 and Botsch et al. 2010 for details.

IV. Experiments and Results

Figure 3 through Figure 7 show a comparison of the geometric multigrid solver against a standard Gauss-Seidel solver with respect to the number of iterations for various surface meshes. The iterative process stopped when either the residual was below a certain threshold or after a number of iterations. For all the experiments, the threshold used was \(\epsilon = 10^{-11}\) and the maximum number of iterations was \(3000\). For the geometric multigrid solver, the plots show the total number of smoothing iterations, and not the total number of V-Cycles. In all experiments, \(5\) pre-smoothing and \(5\) post-smoothing iterations were used for the geometric multigrid solver.

As can be seen in the plots of Figure 3 to Figure 7, the Gauss-Seidel stopped due to the maximum iterations criteria for all but one experiment (Figure 3, Spot (Low Poly)). For all the others, the solution found is above the specified threshold. In contrast, the geometric multigrid solver quickly converges to a solution below the desired threshold.

Figure 3: Comparison of the rate of convergence between the Geometric Multigrid solver (left) and the Gauss-Seidel (right) for the Spot (Low Poly) model.
Figure 4: Comparison of the rate of convergence between the Geometric Multigrid solver (left) and the Gauss-Seidel (right) for the Cow model.
Figure 5: Comparison of the rate of convergence between the Geometric Multigrid solver (left) and the Gauss-Seidel (right) for the Stanford Bunny (Low Poly) model.
Figure 6: Comparison of the rate of convergence between the Geometric Multigrid solver (left) and the Gauss-Seidel (right) for the Bratty Dragon model.
Figure 7: Comparison of the rate of convergence between the Geometric Multigrid solver (left) and the Gauss-Seidel (right) for the Armadillo model.

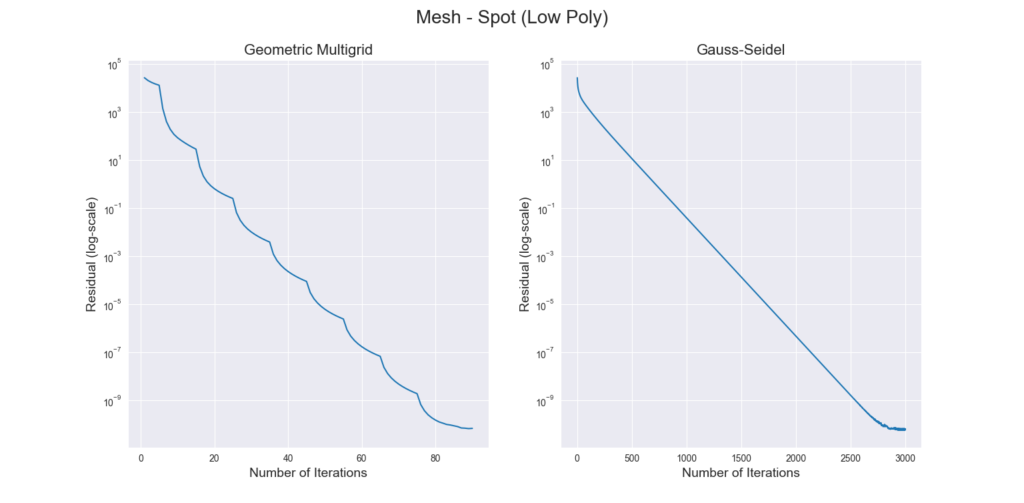
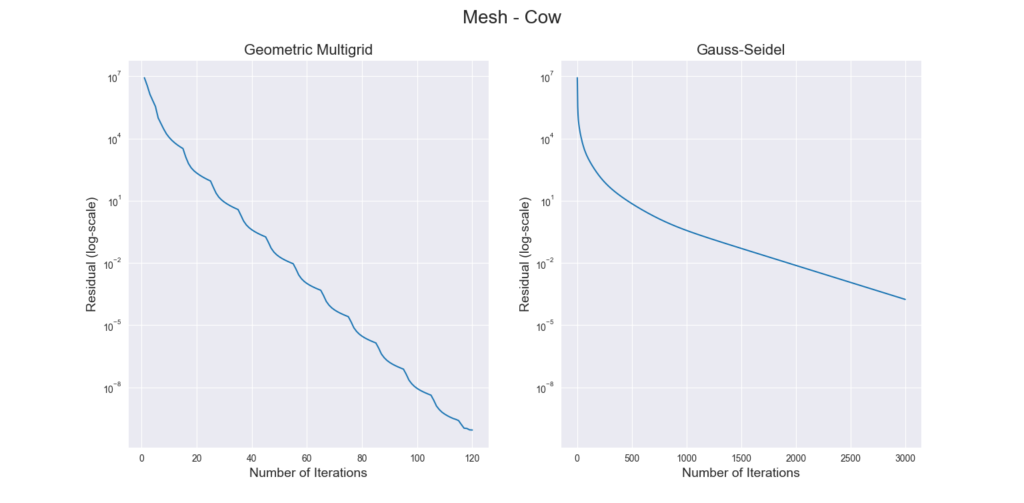
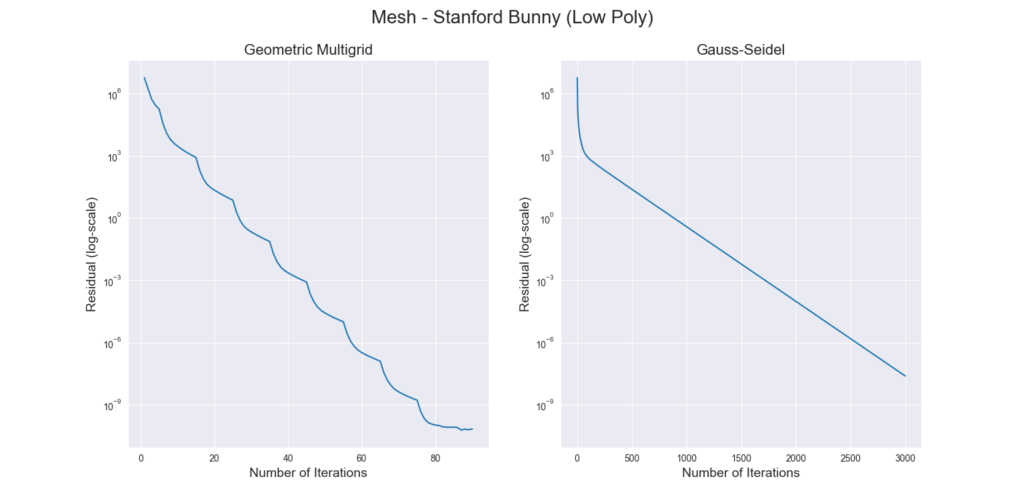
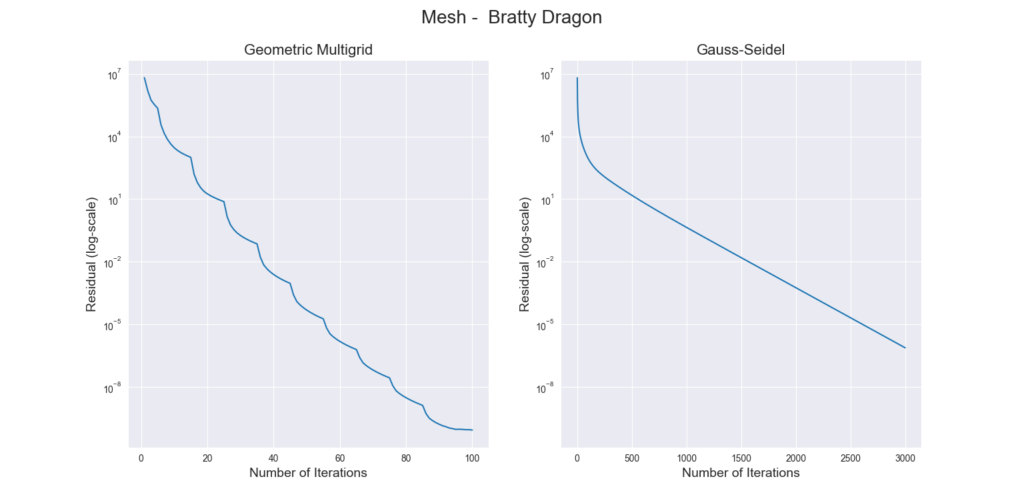
Figure 8 presents a visual comparison of a ground-truth solution (Figure 8, left) and the solutions found by the geometric multigrid solver (Figure 8, center) and the Gauss-Seidel solver (Figure 8, right). The geometric multigrid matches more closely the expected solution, while the solution computed by the Gauss-Seidel solver fails to correctly spread the heat distribution.

Figure 8: Visual comparison of a ground-truth solution (left) and the solution found for the heat equation using a geometric multigrid solver (center) and Gauss-Seidel solver (right).

Finally, Figure 9 and Figure 10 compare the execution time of the geometric multigrid solver against the Gauss-Seidel solver. However, the multigrid method requires the construction of a hierarchy of meshes through the mesh simplification algorithm, which is not required for the Gauss-Seidel method. As the results demonstrate, the geometric multigrid version is faster than the Gauss-Seidel method even when the time to compute the successive self-parameterization is taken into account.

One limitation of our MATLAB implementation is that the system runs out of memory for some of the input meshes. To run all the experiments with the same parameters, we limited the hierarchy depth to two, which would correspond to a two-grid algorithm. However, Heath 2018 mentions that deeper hierarchies can make the computation progressively faster. Hence, we could expect even better results using an optimized implementation.

Figure 9: Time comparison between the geometric multigrid solver and Gauss-Seidel for the Armadillo, Bratty Dragon, and Cow models. For the geometric multigrid version, the mesh simplification time is an additional step that is not required for Gauss-Seidel. Even when the simplification is taken into account, the geometric multigrid method is significantly faster than the Gauss-Seidel solver.
Figure 10: Time comparison between the geometric multigrid solver and Gauss-Seidel for the Stanford Bunny (Low Poly) and Spot (Low Poly) models. For the geometric multigrid version, the mesh simplification time is an additional step that is not required for Gauss-Seidel. Even when the simplification is taken into account, the geometric multigrid method is significantly faster than the Gauss-Seidel solver.

V. Conclusions and Future Work

In this post we report the results obtained for the geometric multigrid solver for curved meshes, which was one of the original goals of the SGI project proposal. With this, the SGI project can be considered complete. The implementation may be improved in various aspects, especially regarding memory usage, which was a critical bottleneck in our case. For this, an implementation in a low-level language that provides fine-grained control over memory allocation and deallocation may be fruitful. Moreover, a comparison with Wiersma et al. 2023 could be an interesting direction for further studies in the area and to investigate new research ideas.

We would like to profusely thank Paul Kry for the mentoring, including the patience to keep answering questions after the two weeks scheduled for the project.

VI. References

Liu, H., Zhang, J., Ben-Chen, M. & Jacobson, A. Surface Multigrid via Intrinsic Prolongation. ACM Trans. Graph. 40 (2021).

Solomon, Justin. Numerical algorithms: methods for computer vision, machine learning, and graphics. CRC press, 2015.

Heath, Michael T. Scientific computing: an introductory survey, revised second edition. Society for Industrial and Applied Mathematics, 2018.

Crane, Keenan, Clarisse Weischedel, and Max Wardetzky. “Geodesics in heat: A new approach to computing distance based on heat flow.” ACM Transactions on Graphics (TOG) 32.5 (2013): 1-11.

Botsch, Mario, et al. Polygon mesh processing. CRC press, 2010.

Brandt, Achi. “Multi-level adaptive solutions to boundary-value problems.” Mathematics of computation 31.138 (1977): 333-390.

Liu, H., Kim, V., Chaudhuri, S., Aigerman, N. \& Jacobson, A. Neural Subdivision. ACM Trans. Graph.. 39 (2020).

Wiersma, Ruben, et al. “A Fast Geometric Multigrid Method for Curved Surfaces.” ACM SIGGRAPH 2023 Conference Proceedings. 2023.

Categories
Research

The (in)accurate Gradients of Neural Representations

Students: Gabriele Dominici, Daniel Perazzo, Munshi Sanowar Raihan, João Teixeira

TA: Nursena Koprucu

Mentors: Peter Yichen Chen, Rundi Wu, Honglin Chen, Ishit Mehta, Eitan Grinspun

1. Introduction

Implicit neural representation promises infinite resolution, automatic gradients, and memory efficiency. In practice, however, these promises often do not hold. Our project explored one specific drawback of implicit neural representations: the noisy gradient. The source code of this project is available on our GitHub repository.

The noisy gradient problem of neural representation has been observed in the context of solving PDEs [1], geometry processing [2,3], topology optimization [4], and 3D reconstruction [5].

1.1. Motivational Example: 1D advection

Our goal is to solve time-dependent PDEs on neural network-based spatial representations. Let’s consider the classic 1D advection equation:

This equation describes the passive advection of some scalar field u carried along at a constant speed a.

Fig 1: Advected scalar field (left), and gradient of the advected quantity (right) over time.

We will parameterize each time-discretized spatial field with a neural network. The field quantity at an arbitrary location can be queried via network inference f(x). The weights of this network are updated at each time step with optimization-based time integration [1]. 

1.2. The Problem: Noisy Gradients

   Fig 2: Comparisons of advected values and gradients of different neural representations. Ground truth (top row), the sine activation (middle row), and the Gaussian activation (bottom row).

Following the INSR literature, we explore different activation functions for our neural network-based scalar field. The figure above compares the predicted scalar quantity and their gradients for both sine [8] and Gaussian [12] activation networks. The predicted scalar quantity matches the ground truth well in all cases. But the gradient of the advected quantity is extremely noisy regardless of the choice of the activation function.

In the subsequent sections, we will tackle this problem using several approaches that fall into two categories: pure neural representation (Section 2) and hybrid grid-neural representations (Section 3).

2. Pure Neural Representations

2.1 Tuning Omega

Fig 3: Large omega values cause noisy gradients, while small omega values give smoother gradients.

The omega hyperparameter controls the frequency range that the SIREN network learns [8]. In general, if we reduce the value of omega, the gradients learned by the networks become less noisy. As seen in the figure above, choosing omega = 5 ensures the network has smooth gradients, while choosing a larger value like 50 gives us very noisy gradients. However, finding the optimal omega value is a non-trivial task. Users need to tune this parameter for each problem.

2.2. Finite Differences

Fig 4: Gradients estimated by finite difference method.

Instead of calculating the gradients by taking the derivative of the output with respect to the inputs using autodiff, we can also use finite differences to approximate the gradients. Because finite difference stencils have local compact supports, they are less susceptible to noise. Indeed, the gradients of the finite difference solution are much less noisy than the autodiff version (see figure above).

2.3 Averaging

Fig 5: Evolving of the gradient of the function over time in the mean gradients approach.

Instead of using the gradients computed by autodiff, we spatially average them by calculating the mean at four more neighboring points for each location.  Although the gradients seem smoother at the very beginning, it is easy to see that after a few timesteps, the gradient’s peaks become fictitiously taller, degrading the results (Fig 5). 

2.4 Initializing with Ground Truth Gradients

Fig 6: Evolving of the gradient of the function over time where the gradients are initialized to be the ground truth gradients.

At timestep 0, the neural network is trained to predict the initial values of the function we are trying to optimize. In addition, similarly to what is done in Sobolev training [6], we force the model to have the same gradients as the desired function. 

This method does reduce the noise in the gradient over time (Fig 6), but the information gathered from the extra supervision used in the initialization steps slowly dissolves. Furthermore, these gradients are not always available or not suitable for setting up a loss function in such a manner, making this solution not always applicable. 

3. Hybrid grid-neural representations

Fig 7: Description of the multi-resolution hashgrid (reproduced from [7]).

To address neural representations’ long training time, Muller et al. [7] developed a multi-resolution hash grid approach: instantNGP. In the following section, we explore instantNGP’s gradient quality. We benchmark it on a 2D fluid example. The figure below shows the example’s initial condition:

Fig 8: Vortex velocity field (reproduced from [1]).

When we try to fit this initial condition using a pure neural representation (i.e., NOT instantNGP), we observe highly noisy gradients, consistent with the results reported in Section 2.1.

Fig 9: Gradient we obtained using pure neural representations for the proposed 2D vortex problem.

Next, we investigated hybrid neural-grid representations, varying the type of the grids and the type of the hash (See Fig 10). 

Fig 10: Different gradients for different resolutions.

The parameters outlined in green obtained the best result. In this case, we use a base resolution of 256 and a 3-level hash grid. 

However, those results only accounted for the initial conditions. If we let the gradients evolve for 99 timesteps according to the PDE, we observe that the gradients start diverging, as can be seen in the video below.

Fig 11: Evolution of the gradients for the 2D fluids for the two vortices example. This test was done with a dense grid of 512 resolution.

In summary, although our hybrid approach seems excellent for the first timesteps, it also appears to limit the expressivity of the network during subsequent evolution.

Due to these problems in the 2D Fluid scenario, we investigated the gradients’ performance in another environment: the 2D Advection problem.

Fig 12: Comparison of Gradient Magnitudes for Different methods.

We used the same network configurations (base resolution, number of levels, number of hidden layers, and hidden features) as the 2D Fluid problem. The hybrid neural-grid representation performs significantly worse than the pure neural representation using SIREN (see Fig 12). Here the network is asked to fit the initial condition only.

Next, we tried to tune the configuration parameters. We discovered that the models performed better for the 2D Advection scenario when the number of level is increased. The best result is given by the following parameters:  number of Levels: 16; per Level Scale: 1.5; Base resolution: 16.

Fig 13: Comparison of Gradient Magnitudes for Hash grid’s best parameters.

Even though the hash grid’s performances improved, the figure above demonstrates that the gradients are still much noisier than the pure neural representation (SIREN). 

As such, we conclude that the hybrid grid-neural representation’ performance is not consistently better than the pure neural representation. In fact, it’s sometimes worse, as demonstrated in the 2D advection example.

4. Future Work

Since our tests and other SIREN works [8] show that tuning the omega hyperparameter is essential for the gradient results, one possible next step is to perform automatic gradient tuning, as proposed in meta-learning techniques [9].

Another possible approach is supervising the gradients. Instead of using the original function to compute the gradients, it is possible to use a separate loss function that certifies the correct gradient values over time. Essentially, we aim to write down the evolution equation of the gradient itself and couple this equation with the original PDE.

Future work should also consider a theoretical understanding of the gradient problem. One possible cause for this problem is the global non-compact support of neural networks. This initially motivates us to explore hybrid grid-neural networks. Other works [7, 10, 11] used similar approaches to extract local features to feed into the network, enforcing a locality to the neural network.

5. References

[1] Chen, Honglin, Wu Rundi, Eitan Grinspun, Changxi Zheng, and Peter Yichen Chen. “Implicit Neural Spatial Representations for Time-dependent PDEs.” International Conference on Machine Learning (ICML). 2023.

[2] Mehta, Ishit, Manmohan Chandraker, and Ravi Ramamoorthi.” A level set theory for neural implicit evolution under explicit flows.” European Conference on Computer Vision (ECCV).  2022.

[3] Yang, Guandao, Serge Belongie, Bharath Hariharan, and Vladlen Koltun. “Geometry processing with neural fields.” Neural Information Processing Systems (NeurIPS). 2021.

[4] Zehnder, Jonas, Yue Li, Stelian Coros, and Bernhard Thomaszewski. “Ntopo: Mesh-free topology optimization using implicit neural representations.” Neural Information Processing Systems (NeurIPS). 2021.

[5] Verbin, Dor, Peter Hedman, Ben Mildenhall, Todd Zickler, Jonathan T. Barron, and Pratul P. Srinivasan. “Ref-nerf: Structured view-dependent appearance for neural radiance fields.” Conference on Computer Vision and Pattern Recognition (CVPR).  2022.

[6] Czarnecki, Wojciech M., Simon Osindero, Max Jaderberg, Grzegorz Swirszcz, and Razvan Pascanu. “Sobolev training for neural networks.” Neural Information Processing Systems (NeurIPS). 2017.

[7] Müller, Thomas, Alex Evans, Christoph Schied, and Alexander Keller. “Instant neural graphics primitives with a multiresolution hash encoding.” ACM Transactions on Graphics (ToG) 41. 2022.

[8] Sitzmann, Vincent, Julien Martel, Alexander Bergman, David Lindell, and Gordon Wetzstein. “Implicit neural representations with periodic activation functions.” Neural Information Processing Systems (NeurIPS). 2020.

[9] Hospedales, Timothy, Antreas Antoniou, Paul Micaelli, and Amos Storkey. “Meta-learning in neural networks: A survey.” IEEE transactions on pattern analysis and machine intelligence 44.9. 2021.

[10] Sun, Cheng, Min Sun, and Hwann-Tzong Chen. “Direct voxel grid optimization: Super-fast convergence for radiance fields reconstruction.” Conference on Computer Vision and Pattern Recognition (CVPR). 2022.

[11] Barron, Jonathan T., Ben Mildenhall, Dor Verbin, Pratul P. Srinivasan, and Peter Hedman. “Zip-NeRF: Anti-aliased grid-based neural radiance fields.”  International Conference on Computer Vision (ICCV). 2023.

[12] Shin-Fang Chng, Sameera Ramasinghe, Jamie Sherrah, Simon Lucey. “Gaussian Activated Radiance Fields for High Fidelity Reconstruction and Pose Estimation” The European Conference on Computer Vision (ECCV). 2022.